【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
(1)求出2019年的利润![]() (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额![]() 成本)
成本)
(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
参考答案:
【答案】(1)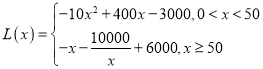 ;(2)2019年年产量为100百辆时,企业所获利润最大,最大利润为5800万元.
;(2)2019年年产量为100百辆时,企业所获利润最大,最大利润为5800万元.
【解析】
(1)先阅读题意,再分当![]() 时,当
时,当![]() 时,求函数解析式即可;
时,求函数解析式即可;
(2)当![]() 时,利用配方法求二次函数的最大值,当
时,利用配方法求二次函数的最大值,当![]() 时,利用均值不等式求函数的最大值,一定要注意取等的条件,再综合求分段函数的最大值即可.
时,利用均值不等式求函数的最大值,一定要注意取等的条件,再综合求分段函数的最大值即可.
解:(1)由已知有当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
即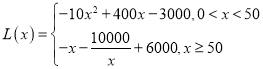 ,
,
(2)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 取最大值
取最大值![]() ,
,
当![]() 时,
时,![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
又![]()
故2019年年产量为100百辆时,企业所获利润最大,最大利润为5800万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)设全集U=A∪B,求(UA)∪(UB);
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有
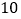 个大小相同的黑球和白球.已知从袋中任意摸出
个大小相同的黑球和白球.已知从袋中任意摸出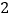 个球,至少得到
个球,至少得到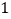 个白球的概率是
个白球的概率是 .
.(1)求白球的个数;
(2)从袋中任意摸出
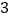 个球,记得到白球的个数为
个球,记得到白球的个数为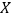 ,求随机变量
,求随机变量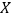 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为
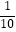 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为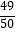 ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
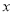 ,
,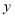 的线性回归直线方程为
的线性回归直线方程为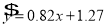 ,且
,且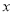 ,
,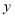 之间的一组相关数据如下表所示,则下列说法错误的为
之间的一组相关数据如下表所示,则下列说法错误的为
A.变量
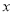 ,
,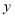 之间呈现正相关关系B.可以预测,当
之间呈现正相关关系B.可以预测,当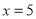 时,
时,
C.
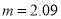 D.由表格数据可知,该回归直线必过点
D.由表格数据可知,该回归直线必过点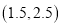
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
①函数
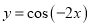 的最小正周期是
的最小正周期是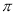 ;
;②在直角坐标系
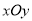 中,点
中,点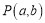 ,将向量
,将向量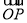 绕点
绕点 逆时针旋转
逆时针旋转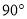 得到向量
得到向量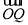 ,则点
,则点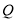 的坐标是
的坐标是 ;
;③在同一直角坐标系中,函数
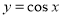 的图象和函数
的图象和函数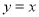 的图象有两个公共点;
的图象有两个公共点;④函数
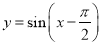 在
在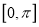 上是增函数.
上是增函数.其中,正确的命题是________(填正确命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=6cos2
 sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形. 
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)= ,且x0∈(﹣
,且x0∈(﹣  ),求f(x0+1)的值.
),求f(x0+1)的值.
相关试题

