【题目】为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况,对全年级2000名高三学生进行了问卷调查,统计结果如下表:
校区 | 愿意参加 | 不愿意参加 |
重庆一中本部校区 | 220 | 980 |
重庆一中大学城校区 | 80 | 720 |
(1)若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人,则大学城校区应抽取几人;
(2)现对愿意参加自主招生的同学组织摸底考试,考试题共有5道题,每题20分,对于这5道题,考生“如花姐”完全会答的有3题,不完全会的有2道,不完全会的每道题她得分![]() 的概率满足:
的概率满足:![]() ,假设解答各题之间没有影响,
,假设解答各题之间没有影响,
①对于一道不完全会的题,求“如花姐”得分的均值![]() ;
;
②试求“如花姐”在本次摸底考试中总得分的数学期望.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
试题分析:(1)由分层抽样的概念得结果;(2)①直接利用公式,可得“如花姐”得分的数学期望;②![]() ,由相互独立事件同时发生的概率计算公式,计算随机变量取每个值时的概率,由期望计算公式得结果.
,由相互独立事件同时发生的概率计算公式,计算随机变量取每个值时的概率,由期望计算公式得结果.
试题解析:(1)大学城校区应抽取![]() 人;
人;
(2)①由题知:对一道不完全会的题,“如花姐”得分的分布列为![]() ,即;
,即;
| 6 | 12 | 18 |
|
|
|
|
所以对于每一道不完全会的题,“如花姐”得分的期望为![]() 分;
分;
②记![]() 为“如花姐”做两道不完全会的题的得分总和,则
为“如花姐”做两道不完全会的题的得分总和,则![]()
![]() ;
;
![]() ;
;
![]() .
.
所以“如花姐”最后得分的期望值为![]() 分.
分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】未知数的个数多余方程个数的方程(组)叫做不定方程,最早提出不定方程的是我国的《九章算术》.实际生活中有很多不定方程的例子,例如“百鸡问题”:公元五世纪末,我国古代数学家张丘建在《算经》中提出了“百鸡问题”:“鸡母一,值钱三;鸡翁一,值钱二;鸡雏二,值钱一.百钱买百鸡,问鸡翁、母、雏各几何?”
算法设计:
(1)设母鸡、公鸡、小鸡数分别为
 、
、 、
、 ,则应满足如下条件:
,则应满足如下条件: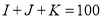 ;
; .
.(2)先分析一下三个变量的可能值.①
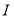 的最小值可能为零,若全部钱用来买母鸡,最多只能买33只,
的最小值可能为零,若全部钱用来买母鸡,最多只能买33只,故
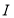 的值为
的值为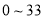 中的整数.②
中的整数.② 的最小值为零,最大值为50.③
的最小值为零,最大值为50.③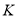 的最小值为零,最大值为100.
的最小值为零,最大值为100.(3)对
 、
、 、
、 三个未知数来说,
三个未知数来说,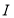 取值范围最少.为提高程序的效率,先考虑对
取值范围最少.为提高程序的效率,先考虑对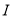 的值进行一一列举.
的值进行一一列举.(4)在固定一个
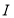 的值的前提下,再对
的值的前提下,再对 值进行一一列举.
值进行一一列举.(5)对于每个
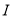 ,
,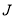 ,怎样去寻找满足百年买百鸡条件的
,怎样去寻找满足百年买百鸡条件的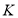 .由于
.由于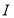 ,
,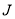 值已设定,便可由下式得到:
值已设定,便可由下式得到: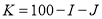 .
.(6)这时的
 ,
,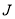 ,
,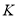 是一组可能解,它只满足“百鸡”条件,还未满足“百钱”.是否真实解,还要看它们是否满足
是一组可能解,它只满足“百鸡”条件,还未满足“百钱”.是否真实解,还要看它们是否满足 ,满足即为所求解.
,满足即为所求解.根据上述算法思想,画出流程图并用伪代码表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有工人1000名,其中250名工人参加短期培训(称为
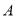 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为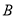 类工人).现用分层抽样方法(按
类工人).现用分层抽样方法(按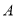 类,
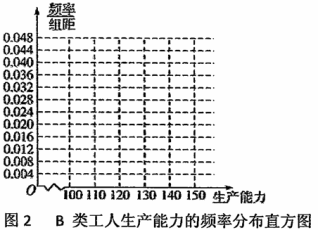
类, 类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).(1)
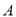 类工人和
类工人和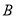 类工人中个抽查多少工人?
类工人中个抽查多少工人?(2)从
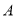 类工人中的抽查结果和从
类工人中的抽查结果和从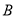 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.表1:

表2:

① 先确定
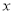 ,
,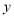 ,再完成下列频率分布直方图,就生产能力而言,
,再完成下列频率分布直方图,就生产能力而言,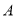 类工人中个体间的差异程度与
类工人中个体间的差异程度与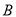 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)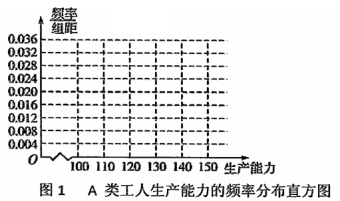
② 分别估计
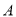 类工人和
类工人和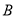 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有5个形状大小完全相同的球,其中有2个红球,3个白球.
(1)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(2)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
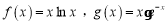 .
.(1)记
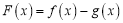 ,求证:函数
,求证:函数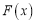 在区间
在区间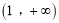 内有且仅有一个零点;
内有且仅有一个零点;(2)用
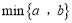 表示
表示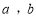 中的最小值,设函数
中的最小值,设函数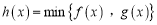 ,若关于
,若关于 的方程
的方程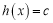 (其中
(其中 为常数)在区间
为常数)在区间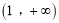 有两个不相等的实根
有两个不相等的实根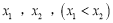 ,记
,记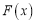 在
在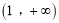 内的零点为
内的零点为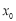 ,试证明:
,试证明: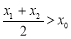 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某校高三上学期期末数学考试成绩中,随机抽取了
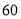 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下: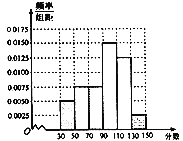
(1)若用分层抽样的方法从分数在
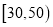 和
和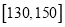 的学生中共抽取
的学生中共抽取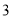 人,该
人,该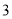 人中成绩在
人中成绩在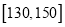 的有几人?
的有几人?(2)在(1)中抽取的
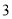 人中,随机抽取
人中,随机抽取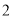 人,求分数在
人,求分数在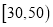 和
和 各
各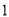 人的概率.
人的概率.(3)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组共抽取4名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率.
相关试题

