【题目】已知函数![]() .
.
(1)记![]() ,求证:函数
,求证:函数![]() 在区间
在区间![]() 内有且仅有一个零点;
内有且仅有一个零点;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,若关于
,若关于![]() 的方程
的方程![]() (其中
(其中![]() 为常数)在区间
为常数)在区间![]() 有两个不相等的实根
有两个不相等的实根![]() ,记
,记![]() 在
在![]() 内的零点为
内的零点为![]() ,试证明:
,试证明:![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)求出函数的导数,通过解关于导函数的不等式,得到函数的单调性,结合零点存在定理证出结论即可;(2)问题转化为证明![]() ,根据
,根据![]() 在
在![]() 上递减,即证明
上递减,即证明![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.
试题解析:(1)证明:![]() ,
,
显然当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,所以由零点存在定理知,
,所以由零点存在定理知,
必存在唯一![]() ,使得
,使得![]() ,
,
即函数![]() 在区间
在区间![]() 内有且仅有一个零点.
内有且仅有一个零点.
(2)由(1)问可知![]() ,且
,且![]() 时,
时,![]() ,
,![]() 时
时![]() ,
,
因此![]() ,
,
其中![]() 满足
满足![]() 即
即![]() ,(事实上
,(事实上![]() ),
),
而![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
因此![]() 在
在![]() ,若方程
,若方程![]() 在区间
在区间![]() 有两个不相等的实根,
有两个不相等的实根,
![]() ,则必有
,则必有![]() ,
,
所证![]()
![]() ,因为
,因为![]() 在
在![]() 单调递减,
单调递减,
所以只需证![]() ,而
,而![]() ,所以只需证
,所以只需证![]() ,
,
即证明:![]() ,
,
构造函数![]() ,
,![]() ,
,
发现![]() ,
,![]() ,
,
下证明![]() 时,
时,![]() 恒成立,
恒成立,
考查函数![]() ,所以
,所以![]() 在
在![]() ,
,
所以一定有![]() ,
,
因此,![]() 时,
时,![]() ,
,
即![]() 在
在![]() ,所以
,所以![]() 时,
时,![]() 即成立了.
即成立了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有工人1000名,其中250名工人参加短期培训(称为
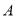 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为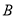 类工人).现用分层抽样方法(按
类工人).现用分层抽样方法(按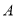 类,
类, 类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).(1)
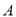 类工人和
类工人和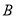 类工人中个抽查多少工人?
类工人中个抽查多少工人?(2)从
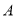 类工人中的抽查结果和从
类工人中的抽查结果和从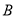 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.表1:

表2:

① 先确定
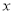 ,
, ,再完成下列频率分布直方图,就生产能力而言,
,再完成下列频率分布直方图,就生产能力而言, 类工人中个体间的差异程度与
类工人中个体间的差异程度与 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)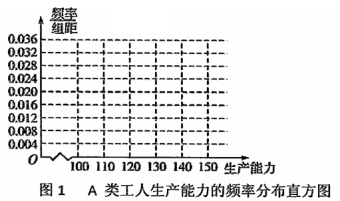
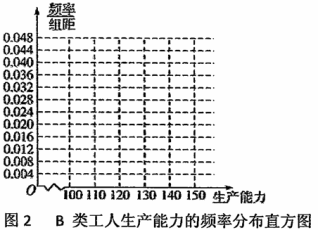
② 分别估计
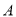 类工人和
类工人和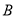 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有5个形状大小完全相同的球,其中有2个红球,3个白球.
(1)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(2)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况,对全年级2000名高三学生进行了问卷调查,统计结果如下表:
校区
愿意参加
不愿意参加
重庆一中本部校区
220
980
重庆一中大学城校区
80
720
(1)若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人,则大学城校区应抽取几人;
(2)现对愿意参加自主招生的同学组织摸底考试,考试题共有5道题,每题20分,对于这5道题,考生“如花姐”完全会答的有3题,不完全会的有2道,不完全会的每道题她得分
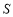 的概率满足:
的概率满足: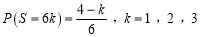 ,假设解答各题之间没有影响,
,假设解答各题之间没有影响,①对于一道不完全会的题,求“如花姐”得分的均值
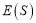 ;
;②试求“如花姐”在本次摸底考试中总得分的数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某校高三上学期期末数学考试成绩中,随机抽取了
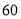 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下: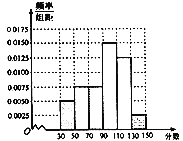
(1)若用分层抽样的方法从分数在
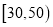 和
和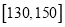 的学生中共抽取
的学生中共抽取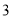 人,该
人,该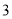 人中成绩在
人中成绩在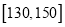 的有几人?
的有几人?(2)在(1)中抽取的
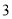 人中,随机抽取
人中,随机抽取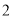 人,求分数在
人,求分数在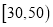 和
和 各
各 人的概率.
人的概率.(3)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组共抽取4名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
相关试题

