【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
参考答案:
【答案】(1)![]() (2)
(2)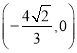
【解析】试题分析:
(1)由题意得![]() ,根据离心率为
,根据离心率为![]() 可得
可得![]() ,故可得到C的方程。(2)由
,故可得到C的方程。(2)由![]() 为线段
为线段![]() 的中点。设
的中点。设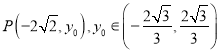 ,当
,当![]() 时,由“点差法”可得直线
时,由“点差法”可得直线![]() 的斜率为
的斜率为![]() ,从而直线
,从而直线![]() 的方程可求得为
的方程可求得为![]()
,过定点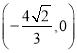 ;当
;当![]() 时,
时, ![]() 过点
过点 。故可得直线
。故可得直线![]() 过点
过点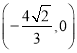 。
。
试题解析:
(1)由题意知![]() ,
,
又椭圆的离心率为![]() ,所以
,所以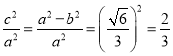 ,
,
所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)因为直线![]() 的方程为
的方程为![]() ,设
,设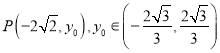 ,
,
①当![]() 时,设
时,设![]() ,显然
,显然![]() ,
,
由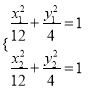 可得
可得![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() 为线段
为线段![]() 的中点,
的中点,
故直线![]() 的斜率为
的斜率为![]() ,
,
又![]() ,
,
所以直线![]() 的方程为
的方程为![]()
即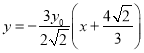 ,显然
,显然![]() 恒过定点
恒过定点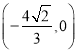 ,
,
②当![]() 时,
时, ![]() 过点
过点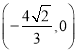 ,
,
综上可得直线![]() 过定点
过定点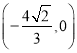 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温
 (℃)与该小卖部的这种饮料销量
(℃)与该小卖部的这种饮料销量 (杯),得到如下数据:
(杯),得到如下数据:日期
1月11日
1月12日
1月13日
1月14日
1月15日
平均气温
 (℃)
(℃)9
10
12
11
8
销量
 (杯)
(杯)23
25
30
26
21
(1)请根据所给五组数据,求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(2)据(1)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(℃),请预测该奶茶店这种饮料的销量.
(参考公式:
 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)﹣g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2﹣3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 的一条弦被点
的一条弦被点 平分,则此弦所在的直线方程是( )
平分,则此弦所在的直线方程是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣1,其中n∈N* .
(1)求数列{an}的通项公式;
(2)设anbn= ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点到准线的距离为
的焦点到准线的距离为 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点 .
.(1)若
 的坐标为
的坐标为 ,求
,求 的值;
的值;(2)设线段
 的中点为
的中点为 ,点
,点 的坐标为
的坐标为 ,过
,过 的直线
的直线 与线段
与线段 为直径的圆相切,切点为
为直径的圆相切,切点为 ,且直线
,且直线 与抛物线
与抛物线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄的频数分布及支持“生育二胎”人数如表:
年龄
[5,15)
[15,25)
[25,35)
[35,45)
[45,55)
[55,65)
频数
5
10
15
10
5
5
支持“生育二胎”
4
5
12
8
2
1
(1)由以上统计数据填下面2乘2列联表,并问是否有的99%把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:
(2)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望;年龄不低于45岁的人数
年龄低于45岁的人数
合计
支持
a=
c=
不支持
b=
d=
合计
参考数据:
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
K2=
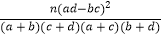 .
.
相关试题

