【题目】设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)﹣g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2﹣3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围 .
参考答案:
【答案】![]()
【解析】解:∵f(x)=x2﹣3x+4与g(x)=2x+m在[0,3]上是“关联函数”,
故函数y=h(x)=f(x)﹣g(x)=x2﹣5x+4﹣m在[0,3]上有两个不同的零点,
故有 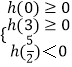 ,即
,即 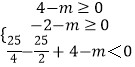 ,解得﹣
,解得﹣ ![]() <m≤﹣2,
<m≤﹣2,
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解函数的值的相关知识,掌握函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法,以及对函数的零点的理解,了解函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 (a∈R)
(a∈R)
(1)若f(x)在x=0处取得极值,确定a的值,并求此时曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)在[3,+∞)上为减函数,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=alnx﹣ax﹣3(a≠0).
(1)讨论f(x)的单调性;
(2)若f(x)+(a+1)x+4﹣e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数);
(3)求证ln(22+1)+ln(32+1)+ln(42+1)+…+ln(n2+1)<1+2lnn!(n≥2,n∈N*)(n!=1×2×3×…×n). -
科目: 来源: 题型:
查看答案和解析>>【题目】三条直线3x+2y+6=0,2x-3m2y+18=0和2mx-3y+12=0围成直角三角形,求实数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知条件p:A={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R},条件q:B={x|x2﹣2x﹣3≤0,x∈R}.
(1)若A∩B={x|0≤x≤3},求实数m的值;
(2)若q是¬p的充分条件,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣
 x3+
x3+  x2﹣2x(a∈R)
x2﹣2x(a∈R)
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f′(x)<2(a﹣1)成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|x2-ax+a2-19=0},B={ x|x2-5x+6=0},C={x|x2+2x-8=0},且

 (A∩B),A∩C=
(A∩B),A∩C= ,求
,求 的值
的值
相关试题

