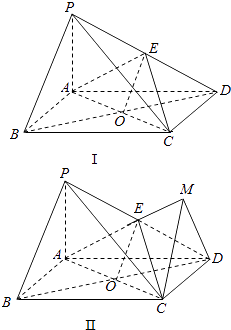
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D﹣AE﹣C为60°,AP=1,AD= ![]() ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.
参考答案:
【答案】(Ⅰ)证明:连接BD交AC于O点,连接EO,∵O为BD中点,E为PD中点,
∴EO∥PB,
EO平面AEC,PB平面AEC,所以PB∥平面AEC;
(Ⅱ)解:延长AE至M连结DM,使得AM⊥DM,
∵四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
∴CD⊥平面AMD,
∵二面角D﹣AE﹣C为60°,
∴∠CMD=60°,
∵AP=1,AD= ![]() ,∠ADP=30°,
,∠ADP=30°,
∴PD=2,
E为PD的中点.AE=1,
∴DM= ![]() ,
,
CD= ![]() =
= ![]() .
.
三棱锥E﹣ACD的体积为: ![]() =
= ![]() =
= ![]() .
.
【解析】(Ⅰ)连接BD交AC于O点,连接EO,只要证明EO∥PB,即可证明PB∥平面AEC;(Ⅱ)延长AE至M连结DM,使得AM⊥DM,说明∠CMD=60°,是二面角的平面角,求出CD,即可三棱锥E﹣ACD的体积.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 (a>0,且a≠1).
(a>0,且a≠1).(1)讨论f(x)的奇偶性;
(2)求a的取值范围,使f(x)>0在定义域上恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f
 =f(x)-f(y),当x>1时,有f(x)>0。
=f(x)-f(y),当x>1时,有f(x)>0。(1)求f(1)的值;
(2)判断f(x)的单调性并证明;
(3)若f(6)=1,解不等式f(x+3)-f
 <2;
<2; (4)若f(4)=2,求f(x)在[1,16]上的值域。
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=1-x2+ln(x+1).
(1)求函数f(x)的单调区间;
(2)若不等式f(x)>
 -x2(k∈N*)在(0,+∞)上恒成立,求k的最大值.
-x2(k∈N*)在(0,+∞)上恒成立,求k的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
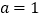 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)若函数
 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数 的取值范围;
的取值范围;(3)设函数
 ,若在区间
,若在区间 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+ax2+bx+c图象上的点P(1,﹣2)处的切线方程为y=﹣3x+1.
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式
(2)若函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos
 ,g(x)=exf(x),其中e为自然对数的底数.
,g(x)=exf(x),其中e为自然对数的底数.
(1)求曲线y=g(x)在点(0,g(0))处的切线方程;
(2)若对任意 时,方程g(x)=xf(x)的解的个数,并说明理由.
时,方程g(x)=xf(x)的解的个数,并说明理由.
相关试题

