【题目】设函数f(x)=1-x2+ln(x+1).
(1)求函数f(x)的单调区间;
(2)若不等式f(x)>![]() -x2(k∈N*)在(0,+∞)上恒成立,求k的最大值.
-x2(k∈N*)在(0,+∞)上恒成立,求k的最大值.
参考答案:
【答案】(1)见解析(2)3
【解析】
(1)首先求出f(x)的定义域,函数f(x)的导数,分别令它大于0,小于0,解不等式,必须注意定义域,求交集;
(2)化简不等式f(x)>![]() ﹣x2,得:(x+1)[1+ln(x+1)]>kx,令g(x)=(x+1))[1+ln(x+1)]﹣kx,求出g'(x),由x>0,求出2+ln(x+1)>2,讨论k,分k≤2,k>2,由恒成立结合单调性判断k的取值,从而得到k的最大值.
﹣x2,得:(x+1)[1+ln(x+1)]>kx,令g(x)=(x+1))[1+ln(x+1)]﹣kx,求出g'(x),由x>0,求出2+ln(x+1)>2,讨论k,分k≤2,k>2,由恒成立结合单调性判断k的取值,从而得到k的最大值.
(1)函数f(x)的定义域为(﹣1,+∞),
函数f(x)的导数f'(x)=﹣2x+![]() ,
,
令f'(x)>0则![]() >2x,
>2x,
解得![]() ,
,
令f'(x)<0则![]() ,
,
解得x>![]() 或x<
或x<![]() ,
,
∵x>﹣1,
∴f(x)的单调增区间为(﹣1,![]() ),
),
单调减区间为(![]() ,+∞);
,+∞);
(2)不等式f(x)>![]() ﹣x2
﹣x2
即1﹣x2+ln(x+1)>![]() ,即1+ln(x+1)>
,即1+ln(x+1)>![]() ,
,
即(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立,
令g(x)=(x+1))[1+ln(x+1)]﹣kx,则
g'(x)=2+ln(x+1)﹣k,
∵x>0,∴2+ln(x+1)>2,
若k≤2,则g'(x)>0,即g(x)在(0,+∞)上递增,
∴g(x)>g(0)即g(x)>1>0,
∴(x+1)[1+ln(x+1)]>kx(k∈N*)在(0,+∞)上恒成立;
若k>2,可以进一步分析,只需满足最小值比0大,即可,
结合K为正整数,故k的最大值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 有三个不同的零点
有三个不同的零点 (其中
(其中 ),则
),则 的值为( )
的值为( )A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 (a>0,且a≠1).
(a>0,且a≠1).(1)讨论f(x)的奇偶性;
(2)求a的取值范围,使f(x)>0在定义域上恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f
 =f(x)-f(y),当x>1时,有f(x)>0。
=f(x)-f(y),当x>1时,有f(x)>0。(1)求f(1)的值;
(2)判断f(x)的单调性并证明;
(3)若f(6)=1,解不等式f(x+3)-f
 <2;
<2; (4)若f(4)=2,求f(x)在[1,16]上的值域。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D﹣AE﹣C为60°,AP=1,AD= ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
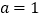 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)若函数
 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数 的取值范围;
的取值范围;(3)设函数
 ,若在区间
,若在区间 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+ax2+bx+c图象上的点P(1,﹣2)处的切线方程为y=﹣3x+1.
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式
(2)若函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围.
相关试题

