【题目】已知函数f(x)=cos ![]() ,g(x)=exf(x),其中e为自然对数的底数.
,g(x)=exf(x),其中e为自然对数的底数.
(1)求曲线y=g(x)在点(0,g(0))处的切线方程;
(2)若对任意 ![]() 时,方程g(x)=xf(x)的解的个数,并说明理由.
时,方程g(x)=xf(x)的解的个数,并说明理由.
参考答案:
【答案】
(1)解:由题意得,f(x)=sinx,g(x)=exsinx,
∴g(0)=e0sin0=0;
g'(x)=ex(cosx+sinx),∴g'(0)=1;
故曲线y=g(x)在点(0,g(0))处的切线方程为y=x
(2)解:设H(x)=g(x)﹣xf(x), ![]() ;
;
则当 ![]() 时,
时,
H'(x)=ex(cosx+sinx)﹣sinx﹣xcosx=(ex﹣x)cosx﹣(ex﹣1)sinx,
当 ![]() ,显然有
,显然有 ![]() ;
;
当 ![]() 时,由
时,由 ![]() ,
,
即有 ![]() ,
,
即有H'(x)<0,
所以当 ![]() 时,总有H'(x)<0,
时,总有H'(x)<0,
故H(x)在 ![]() 上单调递减,
上单调递减,
故函数H(x)在 ![]() 上至多有一个零点;
上至多有一个零点;
又 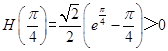 ,
, ![]() ;
;
且H(x)在 ![]() 上是连续不断的,
上是连续不断的,
故函数H(x)在 ![]() 上有且只有一个零点
上有且只有一个零点
【解析】(1)利用导数的几何意义即可求出曲线y=g(x)在点(0,g(0))处的切线方程;(2)构造函数H(x)=g(x)﹣xf(x), ![]() ;利用导数判断函数的单调性,
;利用导数判断函数的单调性,
根据根的存在性定理即可判断函数H(x)在 ![]() 上零点的个数.
上零点的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D﹣AE﹣C为60°,AP=1,AD= ,求三棱锥E﹣ACD的体积.
,求三棱锥E﹣ACD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
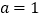 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)若函数
 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数 的取值范围;
的取值范围;(3)设函数
 ,若在区间
,若在区间 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+ax2+bx+c图象上的点P(1,﹣2)处的切线方程为y=﹣3x+1.
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式
(2)若函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A=a1 , a2 , a3 , …,an , 其中ai∈R(1≤i≤n,n>2),l(A)表示和ai+aj(1≤i<j≤n)中所有不同值的个数.
(Ⅰ)设集合P=2,4,6,8,Q=2,4,8,16,分别求l(P)和l(Q);
(Ⅱ)若集合A=2,4,8,…,2n , 求证: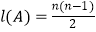 ;
;
(Ⅲ)l(A)是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成角的余弦值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正四棱柱
 中,已知AB=2,
中,已知AB=2, ,
,E、F分别为
 、
、 上的点,且
上的点,且 .
.
(1)求证:BE⊥平面ACF;
(2)求点E到平面ACF的距离.
相关试题

