【题目】设函数y=f(x)的定义域为D,若对于任意x1、x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx﹣3的某一个对称中心,并利用对称中心的上述定义,可得到f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )的值为( )
)的值为( )
A.4027
B.﹣4027
C.8054
D.﹣8054
参考答案:
【答案】D
【解析】解:∵当x=1时,f(1)=1+sinπ﹣3=﹣2,
∴根据对称中心的定义,可得当x1+x2=2时,恒有f(x1)+f(x2)=﹣4,
即a=1,b=﹣2,即函数的对称中心为(1,﹣2)
∴f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )
)
=2013[f( ![]() )+f(
)+f( ![]() )]+f(
)]+f( ![]() )
)
=2013×(﹣4)﹣2=﹣8054,
故选:D.
【考点精析】掌握函数的值是解答本题的根本,需要知道函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】本公司计划2008年在甲,乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲,乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲,乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元,问该公司如何分配在甲,乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
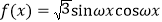
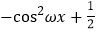 (
( ),与
),与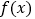 图象的对称轴
图象的对称轴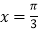 相邻的
相邻的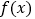 的零点为
的零点为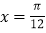 .
.(Ⅰ)讨论函数
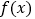 在区间
在区间 上的单调性;
上的单调性;(Ⅱ)设
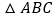 的内角
的内角 ,
,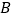 ,
,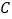 的对应边分别为
的对应边分别为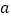 ,
,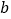 ,
,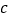 ,且
,且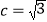 ,
,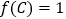 ,若向量
,若向量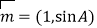 与向量
与向量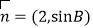 共线,求
共线,求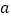 ,
,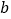 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数f(x)既是奇函数,又是周期为3的周期函数,当x∈(0,
 )时,f(x)=sinπx,f(
)时,f(x)=sinπx,f(  )=0,则函数f(x)在区间[0,6]上的零点个数是( )
)=0,则函数f(x)在区间[0,6]上的零点个数是( )
A.9
B.7
C.5
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的参数方程:
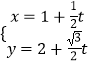 (t为参数),以坐标原点为极点,x轴的正半轴为极轴,且取相同的长度单位建立极坐标系,曲线C的极坐标方程为ρ2=
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,且取相同的长度单位建立极坐标系,曲线C的极坐标方程为ρ2= 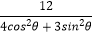 .
.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)设曲线C与直线l交于A,B两点,若P(1,2),求|PA|+|PB|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,且f(x)满足f(x+π)=f(x),当[0,
 )时,f(x)=tanx,则f(
)时,f(x)=tanx,则f(  )= .
)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=aln(2x+1)+bx+1.
(1)若函数y=f(x)在x=1处取得极值,且曲线y=f(x)在点(0,f(0))处的切线与直线2x+y﹣3=0平行,求a的值;
(2)若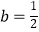 ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性.
相关试题

