【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为![]() .经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
.经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有![]() 个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若![]() ,求
,求![]() 个A级水样本混合化验结果不达标的概率;
个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若![]() ,现有
,现有![]() 个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(II)见解析;(III)见解析.
;(II)见解析;(III)见解析.
【解析】试题分析:(Ⅰ)根据所给相互独立事件重复发生的概率为两相互独立事件概率乘积,及相互独立事件的概率和为![]() ,可得结果;(Ⅱ)分别求出三种方案对应分布列,进一步求出各自的期望值,比较期望值大小得最优方案;(Ⅲ)分别求出期望值,利用期望大小关系建立关于
,可得结果;(Ⅱ)分别求出三种方案对应分布列,进一步求出各自的期望值,比较期望值大小得最优方案;(Ⅲ)分别求出期望值,利用期望大小关系建立关于![]() 的不等式,解得
的不等式,解得![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)该混合样本达标的概率是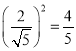 ; 2分
; 2分
所以根据对立事件原理,不达标的概率为![]() .
.
(II)方案一:逐个检测,检测次数为![]() .
.
方案二:由(I)知,每组两个样本的检测时,若达标则检测次数为![]() ,概率为
,概率为![]() ;若不达标则检测次数为
;若不达标则检测次数为![]() ,概率为
,概率为![]() . 故方案二的检测次数
. 故方案二的检测次数![]() ,
, ![]() 可能取
可能取![]() ,
, ![]() ,
, ![]() .概率分布列如下,
.概率分布列如下,
|
|
|
|
|
|
|
|
可求得方案二的期望为![]() ,
,
方案四:混在一起检测,记检测次数为![]() ,
, ![]() 可取
可取![]() ,
, ![]() .概率分布列如下,
.概率分布列如下,
|
|
|
|
|
|
可求得方案四的期望为![]() .
.
比较可得![]() ,故选择方案四最“优”.
,故选择方案四最“优”.
(III)解:方案三:设化验次数![]() ,
, ![]() 可取
可取![]() ,
, ![]() .
.
|
|
|
|
|
|
![]() ;
;
方案四:设化验次数![]() ,
, ![]() 可取
可取![]() ,
, ![]() .
.
|
|
|
|
|
|
![]() ;
;
由题意得![]()
![]() .
.
故当![]() 时,方案三比方案四更“优”.
时,方案三比方案四更“优”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)
(1)求证:对任意m∈R,直线l与⊙C恒有两个交点;
(2)求直线l被⊙C截得的线段的最短长度,及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足:
满足:  .
.(1)求数列
 的通项公式;
的通项公式;(2)若
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
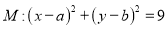 ,
, 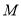 在抛物线
在抛物线 上,圆
上,圆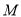 过原点且与
过原点且与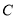 的准线相切.
的准线相切.(Ⅰ) 求
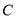 的方程;
的方程;(Ⅱ) 点
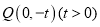 ,点
,点 (与
(与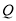 不重合)在直线
不重合)在直线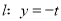 上运动,过点
上运动,过点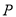 作
作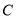 的两条切线,切点分别为
的两条切线,切点分别为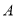 ,
, 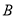 .求证:
.求证: 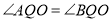 (其中
(其中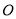 为坐标原点).
为坐标原点). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A{x|
 ≥0},B={x|x2﹣2x﹣3<0},C={x|x2﹣(2a+1)x+a(a+1)<0}.
≥0},B={x|x2﹣2x﹣3<0},C={x|x2﹣(2a+1)x+a(a+1)<0}.
(1)求集合A,B及A∪B;
(2)若C(A∩B),求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=x+b与椭圆
 +y2=1相交于A,B两个不同的点.
+y2=1相交于A,B两个不同的点.
(1)求实数b的取值范围;
(2)已知弦AB的中点P的横坐标是- ,求b的值.
,求b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)在R上的解析式;
(3)求不等式﹣7≤f(x)≤3的解集.
相关试题


