【题目】已知函数f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数f(x)的局部对称点.
(1)若a,b,c∈R,证明函数f(x)=ax3+bx2+cx﹣b必有局部对称点;
(2)是否存在常数m,使得函数f(x)=4x﹣m2x+1+m2﹣3有局部对称点?若存在,求出m的范围,否则说明理由.
参考答案:
【答案】解:(1)证明:由f(x)=ax3+bx2+cx﹣b得f(﹣x)=﹣ax3+bx2﹣cx﹣b,
代入f(﹣x)=﹣f(x) 得ax3+bx2+cx﹣b﹣ax3+bx2﹣cx﹣b=0得到关于x的方程2bx2﹣2b=0,b≠0时,x=±1
当b=0,x∈R等式恒成立,
所以函数f(x)=ax3+bx2+cx﹣b必有局部对称点;
(2)∵f(x)=4x﹣m2x+1+m2﹣3
∴f(﹣x)=4﹣x﹣m2﹣x+1+m2﹣3,
由f(﹣x)=﹣f(x),∴4﹣x﹣m2﹣x+1+m2﹣3=﹣(4x﹣m2x+1+m2﹣3),
于是 4x+4﹣x﹣2m(2x+2﹣x)+2(m2﹣3)=0…(*)在R上有解,
令t=2x+2﹣x(t≥2),则4x+4﹣x=t2﹣2,
∴方程(*)变为t2﹣2mt+2m2﹣8=0 在区间[2,+∞)内有解,需满足条件: ,解得
,解得![]() ,
,
化简得![]() ≤m≤2
≤m≤2![]() .
.
【解析】(1)根据定义构造方程,再判断方程是否有解,问题得以解决.
(2)根据定义构造方程4x+4﹣x﹣2m(2x+2﹣x)+2(m2﹣3)=0…(*)在R上有解,再利用换元法,设t=2x+2﹣x , 方程变形为t2﹣2mt+2m2﹣8=0 在区间[2,+∞)内有解,再根据判别式求出m的范围即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的外接圆半径
的外接圆半径 ,角A、B、C的对边分别是a、b、c,且
,角A、B、C的对边分别是a、b、c,且 .
. (I)求角B和边长b;
(II)求
 面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<
 )一个周期内的图象上的四个点,如图所示,A(﹣
)一个周期内的图象上的四个点,如图所示,A(﹣ , 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,
, 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称, 在x轴方向上的投影为
在x轴方向上的投影为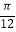 .
.
(1)求函数f(x)的解析式及单调递减区间;
(2)将函数f(x)的图象向左平移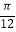 得到函数g(x)的图象,已知g(α)=
得到函数g(x)的图象,已知g(α)= , α∈(﹣
, α∈(﹣ , 0),求g(α+
, 0),求g(α+ )的值.
)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
(1)若成绩小于13秒被认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级800名学生中,成绩属于第三组的人数;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=x2﹣alnx,a∈R.
(1)讨论函数f(x)的单调性;
(2)当a>0时,若f(x)的最小值为1,求a的值;
(3)设g(x)=f(x)﹣2x,若g(x)在[ ,
,  ]有两个极值点x1 , x2(x1<x2),证明:g(x1)﹣g(x2)的取值范围.
]有两个极值点x1 , x2(x1<x2),证明:g(x1)﹣g(x2)的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列
 中,
中, ,前
,前 项和
项和 满足条件
满足条件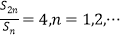 ,
,(1)求数列
 的通项公式和
的通项公式和 ;
;(2)记
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某自行车手从O点出发,沿折线O﹣A﹣B﹣O匀速骑行,其中点A位于点O南偏东45°且与点O相距20
 千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα=
千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα=  ,0°<α<90°)且与点O相距5
,0°<α<90°)且与点O相距5  千米(假设所有路面及观测点都在同一水平面上).
千米(假设所有路面及观测点都在同一水平面上). (1)求该自行车手的骑行速度;
(2)若点O正西方向27.5千米处有个气象观测站E,假定以点E为中心的3.5千米范围内有长时间的持续强降雨.试问:该自行车手会不会进入降雨区,并说明理由.

相关试题

