【题目】已知函数y=x+![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)=![]() ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
参考答案:
【答案】(1) [-4,-3] ;(2) a=![]()
【解析】试题分析:(1)f(x)=![]() =
=![]() ,换元后
,换元后![]()
结合所给性质易得所求;(2)对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立等价于f(x)的值域是g(x)的值域的子集.
试题解析:
(1)y=f(x)=![]() =
=![]() ,
,
设u=2x+1,x∈[0,1],1≤u≤3,
则y=u+![]() -8,u∈[1,3].
-8,u∈[1,3].
由已知性质得,当1≤u≤2,即0≤x≤![]() 时,f(x)单调递减;
时,f(x)单调递减;
所以减区间为[0, ![]() ];
];
当2≤u≤3,即![]() ≤x≤1时,f(x)单调递增;
≤x≤1时,f(x)单调递增;
所以增区间为[![]() ,1];
,1];
由f(0)=-3,f(![]() )=-4,f(1)=-
)=-4,f(1)=-![]() ,
,
得f(x)的值域为[-4,-3].
(2)g(x)=-x-2a为减函数,
故g(x)∈[-1-2a,-2a],x∈[0,1].
由题意,f(x)的值域是g(x)的值域的子集,
∴![]() ∴a=
∴a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是R上的偶函数,且当x>0时,函数的解析式为f(x)=
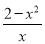 .
.(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求当x<0时,函数的解析式.
-
科目: 来源: 题型:
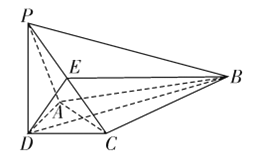
查看答案和解析>>【题目】如图,在四棱锥
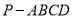 中,
中, 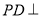 平面
平面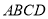 ,
, 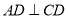 ,
, 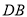 平分
平分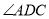 ,
, 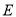 为
为 的中点,
的中点, 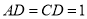 ,
,  .
.
(1)证明:
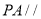 平面
平面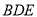 .
.(2)证明:
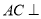 平面
平面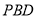 .
.(3)求直线
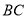 与平面
与平面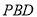 所成的角的正切值.
所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数对
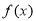 一切实数
一切实数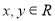 都有
都有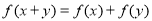 ,且当
,且当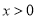 时,
时,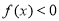 ,又
,又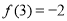 .
.(1)判断该函数的奇偶性并说明理由;、
(2)试判断该函数在
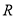 上的单调性;
上的单调性;(3)求
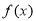 在区间
在区间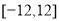 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
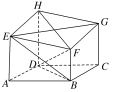
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
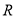 上的函数
上的函数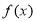 满足:
满足: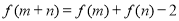 对任意
对任意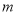 、
、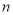
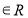 恒成立,当
恒成立,当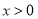 时,
时,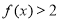 .
.(1)求证
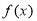 在
在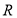 上是单调递增函数;
上是单调递增函数;(2)已知
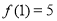 ,解关于
,解关于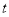 的不等式
的不等式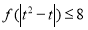 ;
;(3)若
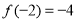 ,且不等式
,且不等式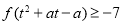 对任意
对任意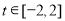 恒成立.求实数
恒成立.求实数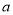 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)甲、乙两袋中各装有大小相同的小球
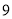 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为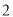 、
、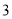 、
、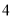 ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为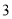 ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量
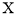 ,求
,求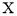 的分布列和数学期望.
的分布列和数学期望.
相关试题

