【题目】已知函数对![]() 一切实数
一切实数![]() 都有
都有![]() ,且当
,且当![]() 时,
时,![]() ,又
,又![]() .
.
(1)判断该函数的奇偶性并说明理由;、
(2)试判断该函数在![]() 上的单调性;
上的单调性;
(3)求![]() 在区间
在区间![]() 的最大值和最小值.
的最大值和最小值.
参考答案:
【答案】(1)![]() 为奇函数.;(2)
为奇函数.;(2)![]() 为
为![]() 上的减函数;(3)最大值是8,最小值是-8.
上的减函数;(3)最大值是8,最小值是-8.
【解析】
试题分析:本题是抽象函数问题,解题时注意赋值法的应用.(1)由于要判断奇偶性,因此要先求得![]()
![]() ,然后想法研究
,然后想法研究![]() 与
与![]() 是什么关系,这只要令
是什么关系,这只要令![]() 即得;(2)要判断单调性,一般设
即得;(2)要判断单调性,一般设![]() ,由已知条件形式,表示出
,由已知条件形式,表示出![]() ,由已知就可得
,由已知就可得![]() ;(3)由(2)得所求最大值为
;(3)由(2)得所求最大值为![]() ,最小值为
,最小值为![]() ,再由
,再由![]() 可得.
可得.
试题解析:(1)令![]() ,得
,得![]() ,
,
∴![]() ,
,
令![]() ,得
,得![]() ,
,
∴![]() ,
,
∴![]() 为奇函数.
为奇函数.
(2)任取![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() 为
为![]() 上的减函数.
上的减函数.
(3)∵![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() 最小,
最小,![]() 最大,
最大,
又![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上的最大值是8,最小值是-8.
上的最大值是8,最小值是-8.
-
科目: 来源: 题型:
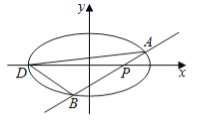
查看答案和解析>>【题目】如图,椭圆

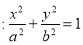 (
(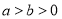 )的离心率是
)的离心率是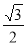 ,过点
,过点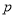 (
(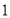 ,
, )的动直线
)的动直线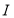 与椭圆相交于
与椭圆相交于 ,
,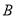 两点,当直线
两点,当直线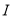 平行于
平行于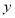 轴时,直线
轴时,直线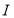 被椭圆
被椭圆 截得的线段长为
截得的线段长为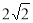 .
.
⑴求椭圆
 的方程:
的方程:⑵已知
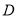 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线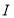 使得
使得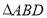 的面积为
的面积为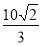 ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是R上的偶函数,且当x>0时,函数的解析式为f(x)=
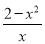 .
.(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求当x<0时,函数的解析式.
-
科目: 来源: 题型:
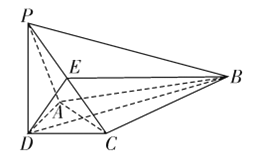
查看答案和解析>>【题目】如图,在四棱锥
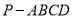 中,
中, 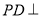 平面
平面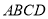 ,
, 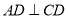 ,
, 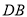 平分
平分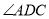 ,
, 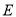 为
为 的中点,
的中点, 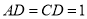 ,
,  .
.
(1)证明:
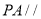 平面
平面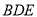 .
.(2)证明:
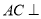 平面
平面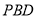 .
.(3)求直线
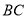 与平面
与平面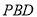 所成的角的正切值.
所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x+
 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, 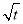 ]上是减函数,在[
]上是减函数,在[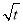 ,+∞)上是增函数.
,+∞)上是增函数.(1)已知f(x)=
 ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
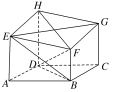
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
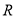 上的函数
上的函数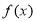 满足:
满足: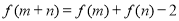 对任意
对任意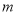 、
、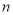
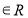 恒成立,当
恒成立,当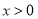 时,
时,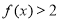 .
.(1)求证
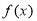 在
在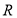 上是单调递增函数;
上是单调递增函数;(2)已知
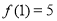 ,解关于
,解关于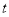 的不等式
的不等式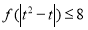 ;
;(3)若
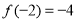 ,且不等式
,且不等式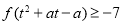 对任意
对任意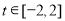 恒成立.求实数
恒成立.求实数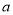 的取值范围.
的取值范围.
相关试题

