【题目】(本小题满分12分)甲、乙两袋中各装有大小相同的小球![]() 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为![]() 、
、![]() 、
、![]() ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为![]() ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)![]() ;(2)分布列见解析,数学期望是
;(2)分布列见解析,数学期望是![]() .
.
【解析】
试题分析:(1)设事件A为“两手所取的球不同色”,由此能求出P(A);(2)依题意,X的可能取值为0,1,2,左手所取的两球颜色相同的概率为![]() ,右手所取的两球颜色相同的概率为
,右手所取的两球颜色相同的概率为![]() ,分别求出P(X=0),P(X=1),P(X=2),由此能求出X的分布列和EX.
,分别求出P(X=0),P(X=1),P(X=2),由此能求出X的分布列和EX.
试题解析:(1)设事件![]() 为“两手所取的球不同色”,
为“两手所取的球不同色”,
则![]()
(2)依题意,![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() .
.
左手所取的两球颜色相同的概率为![]()
右手所取的两球颜色相同的概率为![]()
![]()
![]()
![]()
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x+
 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, 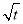 ]上是减函数,在[
]上是减函数,在[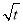 ,+∞)上是增函数.
,+∞)上是增函数.(1)已知f(x)=
 ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
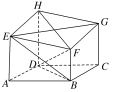
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
 上的函数
上的函数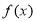 满足:
满足: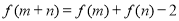 对任意
对任意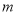 、
、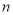
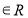 恒成立,当
恒成立,当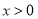 时,
时,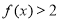 .
.(1)求证
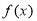 在
在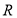 上是单调递增函数;
上是单调递增函数;(2)已知
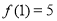 ,解关于
,解关于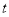 的不等式
的不等式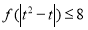 ;
;(3)若
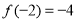 ,且不等式
,且不等式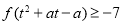 对任意
对任意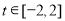 恒成立.求实数
恒成立.求实数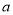 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】用0,1,2, 3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的五位数?
(3)能组成多少个无重复数字且比1325大的四位数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
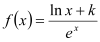 (
(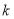 为常数,
为常数,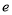 =2.71828……是自然对数的底数),曲线
=2.71828……是自然对数的底数),曲线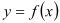 在点
在点 处的切线与
处的切线与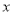 轴平行.
轴平行.(1)求
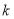 的值;
的值;(2)求
 的单调区间;
的单调区间;(3)设
 ,其中
,其中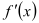 是
是 的导函数.证明:对任意
的导函数.证明:对任意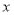 >0,
>0,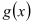 <
<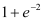 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
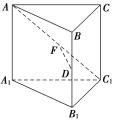
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
相关试题

