【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
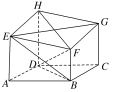
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
参考答案:
【答案】见解析
【解析】解:(1)证明:连接AC,由AE ![]() CG可知四边形AEGC为平行四边形.
CG可知四边形AEGC为平行四边形.
所以EG∥AC,而AC⊥BD,AC⊥BF,所以EG⊥BD,EG⊥BF,
因为BD∩BF=B,所以EG⊥平面BDHF,又DF平面BDHF,所以EG⊥DF。
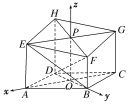
(2)设AC∩BD=O,EG∩HF=P,由已知可得:平面ADHE∥平面BCGF,所以EH∥FG,同理可得:EF∥HG,所以四边形EFGH为平行四边形,所以P为EG的中点,O为AC的中点,所以OP綊AE,
从而OP⊥平面ABCD,
又OA⊥OB,所以OA,OB,OP两两垂直,由平面几何知识,得BF=2。
如图,建立空间直角坐标系Oxyz,则B(0,2,0),E(2![]() ,0,3),F(0,2,2),P(0,0,3),
,0,3),F(0,2,2),P(0,0,3),
所以![]() =(2
=(2![]() ,-2,3),
,-2,3),![]() =(2
=(2![]() ,0,0,),
,0,0,),![]() =(0,2,-1).
=(0,2,-1).
设平面EFGH的法向量为n=(x,y,z),
![]()
可得![]()
令y=1,则z=2。
所以n=(0,1,2).
设BE与平面EFGH所成角为θ,则sin θ=![]() =
=![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
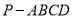 中,
中, 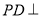 平面
平面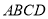 ,
, 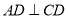 ,
, 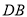 平分
平分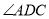 ,
, 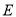 为
为 的中点,
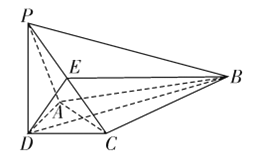
的中点, 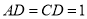 ,
,  .
.
(1)证明:
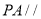 平面
平面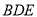 .
.(2)证明:
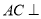 平面
平面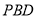 .
.(3)求直线
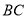 与平面
与平面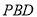 所成的角的正切值.
所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数对
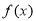 一切实数
一切实数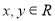 都有
都有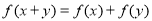 ,且当
,且当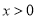 时,
时,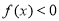 ,又
,又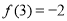 .
.(1)判断该函数的奇偶性并说明理由;、
(2)试判断该函数在
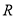 上的单调性;
上的单调性;(3)求
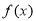 在区间
在区间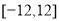 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x+
 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, 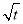 ]上是减函数,在[
]上是减函数,在[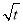 ,+∞)上是增函数.
,+∞)上是增函数.(1)已知f(x)=
 ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
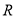 上的函数
上的函数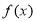 满足:
满足: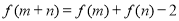 对任意
对任意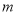 、
、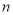
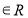 恒成立,当
恒成立,当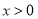 时,
时,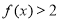 .
.(1)求证
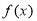 在
在 上是单调递增函数;
上是单调递增函数;(2)已知
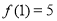 ,解关于
,解关于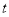 的不等式
的不等式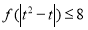 ;
;(3)若
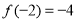 ,且不等式
,且不等式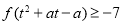 对任意
对任意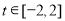 恒成立.求实数
恒成立.求实数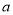 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)甲、乙两袋中各装有大小相同的小球
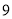 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为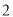 、
、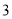 、
、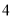 ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为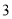 ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量
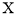 ,求
,求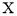 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】用0,1,2, 3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的五位数?
(3)能组成多少个无重复数字且比1325大的四位数?
相关试题

