【题目】下列各组函数中,表示同一函数的是( )
A.![]()
与g(x)=x﹣1
B.f(x)=2|x|与 ![]()
C.![]()
与 ![]()
D.![]()
与 ![]()
参考答案:
【答案】B
【解析】解:对于A: ![]() 的定义域是{x|x≠﹣1},而g(x)=x﹣1的定义域是R,定义域不相同,∴不是同一函数;
的定义域是{x|x≠﹣1},而g(x)=x﹣1的定义域是R,定义域不相同,∴不是同一函数;
对于B:f(x)=2|x|的定义域是R, ![]() =2|x|的定义域是R,定义域相同,对应关系也相同,∴是同一函数;
=2|x|的定义域是R,定义域相同,对应关系也相同,∴是同一函数;
对于C: ![]() =|x|的定义域是R,而
=|x|的定义域是R,而 ![]() 的定义域是{x|x≥0},定义域不相同,对应关系也不相同,∴不是同一函数;
的定义域是{x|x≥0},定义域不相同,对应关系也不相同,∴不是同一函数;
对于D: ![]() 的定义域是{x|﹣1≤x≤1},而
的定义域是{x|﹣1≤x≤1},而 ![]() 的定义域是{x|1≤x或x≤﹣1},定义域不相同,∴不是同一函数;
的定义域是{x|1≤x或x≤﹣1},定义域不相同,∴不是同一函数;
故选B.
【考点精析】根据题目的已知条件,利用判断两个函数是否为同一函数的相关知识可以得到问题的答案,需要掌握只有定义域和对应法则二者完全相同的函数才是同一函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生在假期进行某种小商品的推销,他利用所学知识进行了市场调查,发现这种商品当天的市场价格与他的进货量(件)加上20成反比.已知这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元.若每天的商品都能卖完,求这个学生一天的最大利润是多少?获得最大利润时每天的进货量是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.
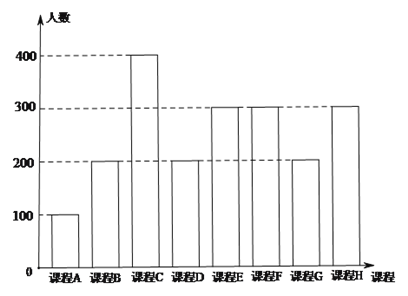
图中,课程
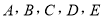 为人文类课程,课程
为人文类课程,课程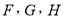 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组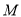 ”).
”).(Ⅰ)在“组
 ”中,选择人文类课程和自然科学类课程的人数各有多少?
”中,选择人文类课程和自然科学类课程的人数各有多少?(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组
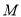 ”中选择
”中选择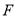 课
课程或
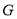 课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择
课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择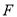 课程的学生中有
课程的学生中有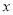 人参加科学营活动,每人需缴纳
人参加科学营活动,每人需缴纳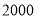 元,选择
元,选择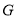 课程的学生中有
课程的学生中有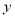 人参加该活动,每人需缴纳
人参加该活动,每人需缴纳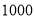 元.记选择
元.记选择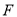 课程和
课程和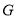 课程的学生自愿报名人数的情况为
课程的学生自愿报名人数的情况为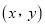 ,参加活动的学生缴纳费用总和为
,参加活动的学生缴纳费用总和为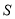 元.
元.①当
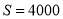 时,写出
时,写出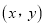 的所有可能取值;
的所有可能取值;②若选择
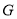 课程的同学都参加科学营活动,求
课程的同学都参加科学营活动,求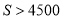 元的概率.
元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x+
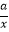 +b,其中a,b是常数且a>0.
+b,其中a,b是常数且a>0.
(1)用函数单调性的定义证明f(x)在区间(0,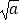 ]上是单调递减函数;
]上是单调递减函数;
(2)已知函数f(x)在区间[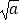 ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】由大于0的自然数构成的等差数列{an},它的最大项为26,其所有项的和为70;
(1)求数列{an}的项数n;
(2)求此数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
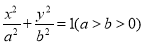 的左右焦点分别为
的左右焦点分别为 ,点
,点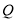 为椭圆上一点.
为椭圆上一点. 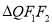 的重心为
的重心为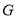 ,内心为
,内心为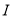 ,且
,且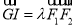 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )A.
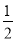 B.
B. 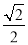 C.
C. 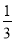 D.
D. 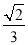
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)当
 时, 求函数
时, 求函数 在区间
在区间 上的最大值.
上的最大值.
相关试题

