【题目】已知函数f(x)=x+ ![]() +b,其中a,b是常数且a>0.
+b,其中a,b是常数且a>0.
(1)用函数单调性的定义证明f(x)在区间(0, ![]() ]上是单调递减函数;
]上是单调递减函数;
(2)已知函数f(x)在区间[ ![]() ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
参考答案:
【答案】
(1)证法一:∵函数f(x)=x+ ![]() +b,其中a,b是常数且a>0,
+b,其中a,b是常数且a>0,
任取设0<x1<x2≤ ![]() ,
,
则x1﹣x2<0,0<x1x2<a,
f(x1)﹣f(x2)=(x1+ ![]() +b)﹣(x2+
+b)﹣(x2+ ![]() +b)=(x1﹣x2)﹣
+b)=(x1﹣x2)﹣ ![]() =(x1﹣x2)
=(x1﹣x2) ![]() >0,
>0,
即f(x1)>f(x2),
∴f(x)在区间(0, ![]() ]上是单调递减函数;
]上是单调递减函数;
证法二:∵函数f(x)=x+ ![]() +b,其中a,b是常数且a>0,
+b,其中a,b是常数且a>0,
∴f′(x)=1﹣ ![]() =
= ![]() ,
,
当x∈(0, ![]() ]时,f′(x)≤0恒成立,
]时,f′(x)≤0恒成立,
故f(x)在区间(0, ![]() ]上是单调递减函数
]上是单调递减函数
(2)已知函数f(x)在区间[ ![]() ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,
当a≤1时,即 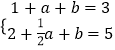 ,解得:a=﹣2(舍去);
,解得:a=﹣2(舍去);
当1<a≤2.25时,即 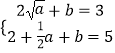 ,解得:a=0(舍去),或:a=16(舍去);
,解得:a=0(舍去),或:a=16(舍去);
当2.25<a<4时, ![]() ,解得:a=3+2
,解得:a=3+2 ![]() (舍去),
(舍去),
当a≥4时,即 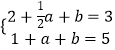 ,解得:a=6;
,解得:a=6;
综上可得:a=6
【解析】(1)证法一:任取设0<x1<x2≤ ![]() ,作差比较可得f(x1)>f(x2),结合函数单调性的定义,可得:f(x)在区间(0,
,作差比较可得f(x1)>f(x2),结合函数单调性的定义,可得:f(x)在区间(0, ![]() ]上是单调递减函数;证法二:求导,分析出当x∈(0,
]上是单调递减函数;证法二:求导,分析出当x∈(0, ![]() ]时,f′(x)≤0恒成立,故f(x)在区间(0,
]时,f′(x)≤0恒成立,故f(x)在区间(0, ![]() ]上是单调递减函数;(2)结合对勾函数的图象和性质,分析函数f(x)在区间[1,2]上f(x)的最值,可求出满足条件的a值.
]上是单调递减函数;(2)结合对勾函数的图象和性质,分析函数f(x)在区间[1,2]上f(x)的最值,可求出满足条件的a值.
【考点精析】掌握函数单调性的判断方法和函数的最值及其几何意义是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x/span>1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
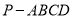 的底面是边长为
的底面是边长为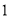 的正方形,
的正方形, 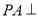 底面
底面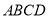 ,
, 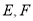 分别为
分别为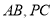 的中点.
的中点.(Ⅰ)求证:
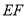
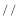 平面
平面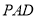 ;
;(Ⅱ)若
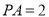 ,试问在线段
,试问在线段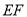 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 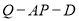 的余弦值为
的余弦值为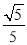 ?若存在,确定点
?若存在,确定点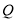 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.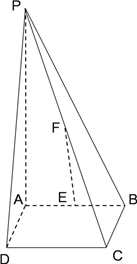
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生在假期进行某种小商品的推销,他利用所学知识进行了市场调查,发现这种商品当天的市场价格与他的进货量(件)加上20成反比.已知这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元.若每天的商品都能卖完,求这个学生一天的最大利润是多少?获得最大利润时每天的进货量是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.
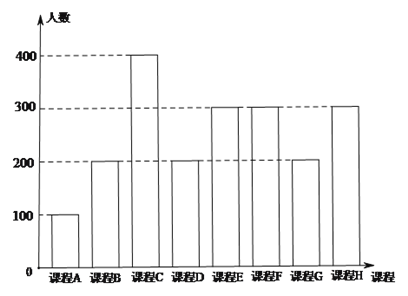
图中,课程
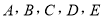 为人文类课程,课程
为人文类课程,课程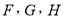 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组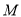 ”).
”).(Ⅰ)在“组
 ”中,选择人文类课程和自然科学类课程的人数各有多少?
”中,选择人文类课程和自然科学类课程的人数各有多少?(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组
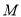 ”中选择
”中选择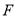 课
课程或
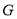 课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择
课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择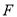 课程的学生中有
课程的学生中有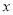 人参加科学营活动,每人需缴纳
人参加科学营活动,每人需缴纳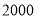 元,选择
元,选择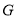 课程的学生中有
课程的学生中有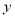 人参加该活动,每人需缴纳
人参加该活动,每人需缴纳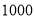 元.记选择
元.记选择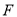 课程和
课程和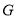 课程的学生自愿报名人数的情况为
课程的学生自愿报名人数的情况为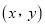 ,参加活动的学生缴纳费用总和为
,参加活动的学生缴纳费用总和为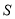 元.
元.①当
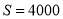 时,写出
时,写出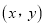 的所有可能取值;
的所有可能取值;②若选择
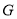 课程的同学都参加科学营活动,求
课程的同学都参加科学营活动,求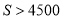 元的概率.
元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.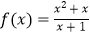
与g(x)=x﹣1
B.f(x)=2|x|与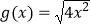
C.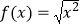
与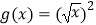
D.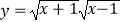
与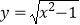
-
科目: 来源: 题型:
查看答案和解析>>【题目】由大于0的自然数构成的等差数列{an},它的最大项为26,其所有项的和为70;
(1)求数列{an}的项数n;
(2)求此数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
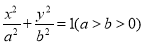 的左右焦点分别为
的左右焦点分别为 ,点
,点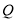 为椭圆上一点.
为椭圆上一点. 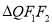 的重心为
的重心为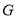 ,内心为
,内心为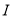 ,且
,且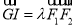 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )A.
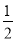 B.
B. 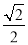 C.
C. 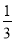 D.
D. 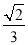
相关试题

