【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.
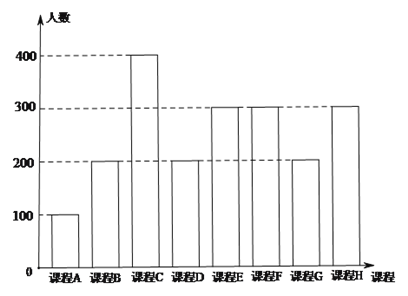
图中,课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组![]() ”).
”).
(Ⅰ)在“组![]() ”中,选择人文类课程和自然科学类课程的人数各有多少?
”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组![]() ”中选择
”中选择![]() 课
课
程或![]() 课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择
课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择![]() 课程的学生中有
课程的学生中有![]() 人参加科学营活动,每人需缴纳
人参加科学营活动,每人需缴纳![]() 元,选择
元,选择![]() 课程的学生中有
课程的学生中有![]() 人参加该活动,每人需缴纳
人参加该活动,每人需缴纳![]() 元.记选择
元.记选择![]() 课程和
课程和![]() 课程的学生自愿报名人数的情况为
课程的学生自愿报名人数的情况为![]() ,参加活动的学生缴纳费用总和为
,参加活动的学生缴纳费用总和为![]() 元.
元.
①当![]() 时,写出
时,写出![]() 的所有可能取值;
的所有可能取值;
②若选择![]() 课程的同学都参加科学营活动,求
课程的同学都参加科学营活动,求![]() 元的概率.
元的概率.
参考答案:
【答案】(Ⅰ) 12,8; (Ⅱ)(ⅰ) ![]() ;(ⅱ)
;(ⅱ) ![]() .
.
【解析】【试题分析】(1)借助题设条件运用题设中提供频率分布直方图进行求解;(2)依据题设借助列举法将所有可能都列举出来,运用古典概型的计算公式进行分析求解:
(Ⅰ)选择人文类课程的人数为(100+200+400+200+300) ![]() 1%=12(人);
1%=12(人);
选择自然科学类课程的人数为(300+200+300) ![]() 1%=8(人).
1%=8(人).
(Ⅱ)(ⅰ)当缴纳费用S=4000时, ![]() 只有两种取值情况:
只有两种取值情况: ![]() ;
;
(ⅱ)设事件![]() 若选择G课程的同学都参加科学营活动,缴纳费用总和S超过4500元.
若选择G课程的同学都参加科学营活动,缴纳费用总和S超过4500元.
在“组M”中,选择F课程和G课程的人数分别为3人和2人.
由于选择G课程的两名同学都参加,下面考虑选择F课程的3位同学参加活动的情况.设每名同学报名参加活动用a表示,不参加活动用b表示,则3名同学报名参加活动的情况共有以下8种情况:aaa,aab,aba,baa,bba,bab,abb,bbb.
当缴纳费用总和S超过4500元时,选择F课程的同学至少要有2名同学参加,有如下4种:aaa,aab,aba,baa.所以, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于无穷数列
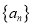 ,记
,记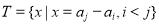 ,若数列
,若数列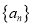 满足:“存在
满足:“存在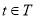 ,使得只要
,使得只要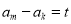 (
(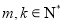 且
且 ),必有
),必有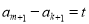 ”,则称数列
”,则称数列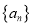 具有性质
具有性质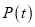 .
.(Ⅰ)若数列
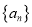 满足
满足 判断数列
判断数列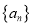 是否具有性质
是否具有性质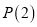 ?是否具有性质
?是否具有性质 ?
?(Ⅱ)求证:“
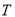 是有限集”是“数列
是有限集”是“数列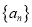 具有性质
具有性质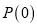 ”的必要不充分条件;
”的必要不充分条件;(Ⅲ)已知
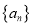 是各项为正整数的数列,且
是各项为正整数的数列,且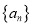 既具有性质
既具有性质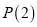 ,又具有性质
,又具有性质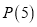 ,求证:存在整数
,求证:存在整数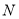 ,使得
,使得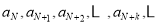 是等差数列.
是等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
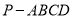 的底面是边长为
的底面是边长为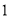 的正方形,
的正方形, 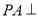 底面
底面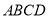 ,
, 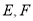 分别为
分别为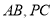 的中点.
的中点.(Ⅰ)求证:
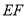
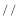 平面
平面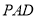 ;
;(Ⅱ)若
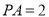 ,试问在线段
,试问在线段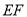 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 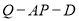 的余弦值为
的余弦值为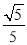 ?若存在,确定点
?若存在,确定点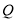 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.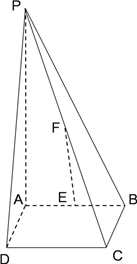
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生在假期进行某种小商品的推销,他利用所学知识进行了市场调查,发现这种商品当天的市场价格与他的进货量(件)加上20成反比.已知这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元.若每天的商品都能卖完,求这个学生一天的最大利润是多少?获得最大利润时每天的进货量是多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x+
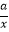 +b,其中a,b是常数且a>0.
+b,其中a,b是常数且a>0.
(1)用函数单调性的定义证明f(x)在区间(0,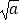 ]上是单调递减函数;
]上是单调递减函数;
(2)已知函数f(x)在区间[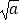 ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.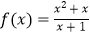
与g(x)=x﹣1
B.f(x)=2|x|与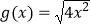
C.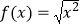
与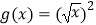
D.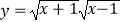
与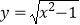
-
科目: 来源: 题型:
查看答案和解析>>【题目】由大于0的自然数构成的等差数列{an},它的最大项为26,其所有项的和为70;
(1)求数列{an}的项数n;
(2)求此数列.
相关试题

