【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时, 求函数
时, 求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
参考答案:
【答案】(Ⅰ)单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】【试题分析】(1)借助题设条件导数与函数的单调性之间的关系求解;(2)先确定函数的极大值,再运用分类整合思想分析求解:
(Ⅰ)由![]() 得
得![]() ,
,
令![]() ,得
,得![]() ,
,
![]() 的情况如下表:
的情况如下表:
|
|
|
|
|
|
| + | 0 |
| 0 | + |
|
| 极大 |
| 极小 |
|
所以函数![]() 的单调区间为
的单调区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(Ⅱ)由![]() 可得
可得![]() .
.
当![]() 即
即![]() 时,由(Ⅰ)可得
时,由(Ⅰ)可得![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
又由(Ⅰ)可知![]() ,
,
所以![]() ;
;
当![]() ,即
,即![]() 时,由(Ⅰ)可得
时,由(Ⅰ)可得![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
当![]() ,即
,即![]() 时,由(Ⅰ)可得
时,由(Ⅰ)可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以,函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
法1:因为![]() ,
,
所以![]() .
.
法2:因为![]() ,
,![]()
所以由(Ⅰ)可知![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() .
.
法3:设![]() ,则
,则![]() ,
,
![]() 的在
的在![]() 上的情况如下表:
上的情况如下表:
| 1 |
|
|
| 2 |
| + | 0 |
| ||
|
|
| 极大 |
|
|
所以,当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]()
所以![]()
![]() .
.
综上讨论,可知:
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.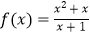
与g(x)=x﹣1
B.f(x)=2|x|与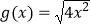
C.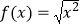
与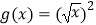
D.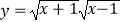
与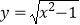
-
科目: 来源: 题型:
查看答案和解析>>【题目】由大于0的自然数构成的等差数列{an},它的最大项为26,其所有项的和为70;
(1)求数列{an}的项数n;
(2)求此数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
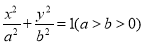 的左右焦点分别为
的左右焦点分别为 ,点
,点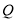 为椭圆上一点.
为椭圆上一点. 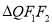 的重心为
的重心为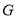 ,内心为
,内心为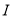 ,且
,且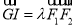 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )A.
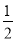 B.
B. 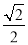 C.
C. 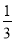 D.
D. 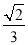
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的左焦点为
的左焦点为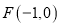 ,
,  为坐标原点,点
为坐标原点,点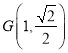 在椭圆上,过点
在椭圆上,过点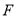 的直线
的直线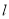 交椭圆于不同的两点
交椭圆于不同的两点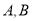 .
.(1)求椭圆
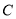 的方程;
的方程;(2)求弦
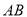 的中点
的中点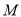 的轨迹方程;
的轨迹方程;(3)设过点
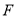 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于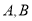 两点,
两点, 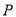 为
为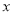 轴上一点,若
轴上一点,若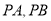 是菱形的两条邻边,求点
是菱形的两条邻边,求点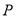 横坐标的取值范围.
横坐标的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
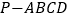 中, 底面
中, 底面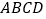 为菱形,
为菱形,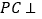 平面
平面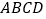 ,点
,点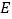 在棱
在棱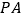 上.
上.(Ⅰ)求证:直线
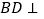 平面
平面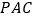 ;
;(Ⅱ)若
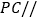 平面
平面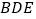 ,求证:
,求证: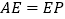 ;
;(Ⅲ)是否存在点
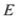 ,使得四面体
,使得四面体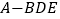 的体积等于四面体
的体积等于四面体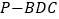 的体积的
的体积的 ?若存在,求出
?若存在,求出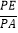 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.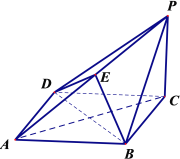
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
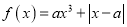 ,
, 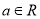 .
.(Ⅰ)若
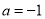 ,求函数
,求函数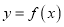 在
在 的单调区间;
的单调区间;(Ⅱ)方程
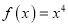 有3个不同的实根,求实数
有3个不同的实根,求实数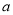 的取值范围;
的取值范围;(Ⅲ)当
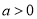 时,若对于任意的
时,若对于任意的 ,都存在
,都存在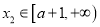 ,使得
,使得 ,求满足条件的正整数
,求满足条件的正整数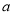 的取值的集合.
的取值的集合.
相关试题

