【题目】已知函数![]() ,其中
,其中![]() 且
且![]() .
.
(Ⅰ)讨论![]() 的单调区间;
的单调区间;
(Ⅱ)若直线![]() 的图象恒在函数
的图象恒在函数![]() 图像的上方,求
图像的上方,求![]() 的取值范围;
的取值范围;
(Ⅲ)若存在![]() ,
,![]() ,使得
,使得![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(I)![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数;(II)
是减函数;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】
试题分析:(I)求函数的导数,利用函数的单调性与导数的关系,即可求解函数![]() 的单调区间;(II)根据直线
的单调区间;(II)根据直线![]() 的图象恒在函数
的图象恒在函数![]() 图像的上方,转化为
图像的上方,转化为![]() 恒成,即可求解
恒成,即可求解![]() 的取值范围;(III)利用函数的单调性和函数零点之间的关系,构造函数利用函数的单调性即可证明结论.
的取值范围;(III)利用函数的单调性和函数零点之间的关系,构造函数利用函数的单调性即可证明结论.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() .
.
期导数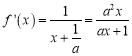 …………………1分
…………………1分
①当![]() 时,
时,![]() ,函数在
,函数在![]() 上是增函数;…………2分
上是增函数;…………2分
②当![]() 时,在区间
时,在区间![]() 上,
上,![]() ;在区间
;在区间![]() 上,
上,![]() .
.
所以在![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数,………………4分
是减函数,………………4分
(Ⅱ)当![]() 时,取
时,取![]() ,则
,则![]() ,不合题意.
,不合题意.
当![]() 时,令
时,令![]() ,则
,则![]() ………………6分
………………6分
问题化为求![]() 恒成立时
恒成立时![]() 的取值范围.
的取值范围.
由于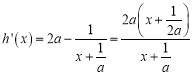 …………………7分
…………………7分
∴在区间![]() 上,
上,![]() ;在区间
;在区间![]() 上,
上,![]()
∴![]() 的最小值为
的最小值为![]() ,
,
所以只需![]() ,即
,即![]()
∴![]() 即
即![]() …………9分
…………9分
(Ⅲ)由于当![]() 时函数在
时函数在![]() 上是增函数,不满足题意,所以
上是增函数,不满足题意,所以![]()
构造函数![]()
∴![]() …………………11分
…………………11分
则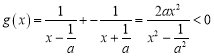 ,所以函数在区间
,所以函数在区间![]() 上为减函数.
上为减函数.
∵![]() ,则
,则![]()
于是![]() ,又
,又![]() ,
,![]() ,
,
由![]() 在
在![]() 上减函数可知
上减函数可知![]() ,即
,即![]() …………14分
…………14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
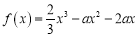 ,其中
,其中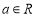 .
.(Ⅰ)若
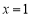 是函数
是函数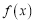 的极值点,求
的极值点,求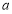 的值;
的值;(Ⅱ)若
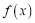 在区间
在区间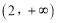 上单调递增,求
上单调递增,求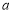 的取值范围;
的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】对定义在区间
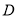 上的函数
上的函数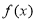 和
和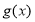 ,如果对任意
,如果对任意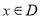 ,都有
,都有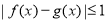 成立,那么称函数
成立,那么称函数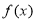 在区间
在区间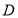 上可被
上可被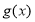 替代,
替代,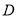 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:①
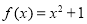 在区间
在区间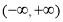 上可被
上可被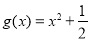 替代;
替代;②
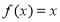 可被
可被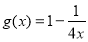 替代的一个“替代区间”为
替代的一个“替代区间”为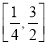 ;
;③
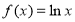 在区间
在区间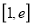 可被
可被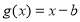 替代,则
替代,则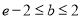 ;
;④
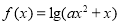 (
(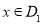 ),
),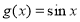 (
(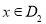 ),则存在实数
),则存在实数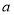 (
(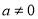 ),使得
),使得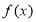 在区间
在区间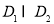 上被
上被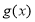 替代; 其中真命题有 .
替代; 其中真命题有 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
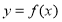 在
在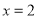 处取得极小值,求
处取得极小值,求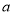 的值;
的值;(2)若
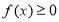 在
在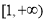 上恒成立,求
上恒成立,求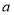 的取值范围;
的取值范围;(3)求证:当
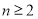 时,
时,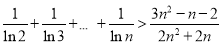 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
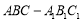 中,
中, ,
,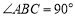 ,
,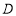 是
是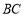 的中点.
的中点. 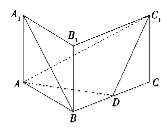
⑴求证:
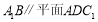 ;
;⑵求二面角
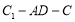 的余弦值;
的余弦值; -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
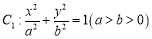 的左、右焦点分别是
的左、右焦点分别是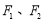 ,下顶点为
,下顶点为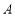 ,线段
,线段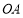 的中点为
的中点为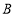 (
(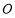 为坐标原点),如图,若抛物线
为坐标原点),如图,若抛物线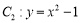 与
与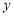 轴的交点为
轴的交点为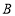 ,且经过
,且经过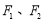 点.
点.
(1)求椭圆
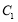 的方程;
的方程;(2)设
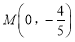 ,
,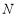 为抛物线
为抛物线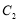 上的一动点,过点
上的一动点,过点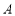 作抛物线
作抛物线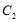 的切线交椭圆
的切线交椭圆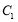 于点
于点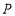 、
、 两点,求
两点,求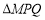 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 :
: 内有一点
内有一点 ,过点
,过点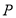 作直线
作直线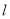 交圆
交圆 于
于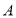 、
、 两点.
两点.(1)当
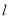 经过圆心
经过圆心 时,求直线
时,求直线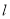 的方程;
的方程;(2)当弦
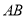 被点
被点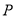 平分时,写出直线
平分时,写出直线 的方程;
的方程;(3)当直线
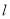 的倾斜角为
的倾斜角为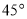 时,求弦
时,求弦 的长.
的长.
相关试题

