【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
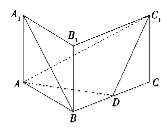
⑴求证:![]() ;
;
⑵求二面角![]() 的余弦值;
的余弦值;
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,根据直四棱柱的性质,得到
,根据直四棱柱的性质,得到![]() ,利用线面平行的判定定理,即可证得
,利用线面平行的判定定理,即可证得![]() ;(2)由
;(2)由![]() 是直棱柱,且
是直棱柱,且![]() ,故
,故![]() 、
、![]() 、
、![]() 两两垂直,建立空间直角坐标系
两两垂直,建立空间直角坐标系![]() ,求解平面
,求解平面![]() 和平面
和平面![]() 的法向量,求解两个向量所成的角,即可求解二面角的余弦值.
的法向量,求解两个向量所成的角,即可求解二面角的余弦值.
试题解析:⑴证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
由![]() 是直三棱柱得四边形
是直三棱柱得四边形![]() 为矩形,
为矩形,![]()
![]() 的中点.
的中点.
又![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中位线,所以
中位线,所以![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() .
.
⑵由![]() 是直棱柱,且
是直棱柱,且![]() ,故
,故![]() 、
、![]() 、
、![]() 两两垂直.
两两垂直.
如图建立空间直角坐标系![]() .
.
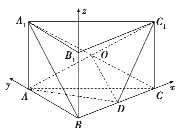
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则有
,则有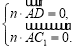 所以
所以![]()
取![]() ,得
,得![]() .
.
易知平面![]() 法向量为
法向量为![]() .
.
由二面角![]() 平面角是锐角,得
平面角是锐角,得![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对定义在区间
 上的函数
上的函数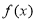 和
和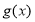 ,如果对任意
,如果对任意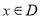 ,都有
,都有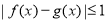 成立,那么称函数
成立,那么称函数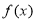 在区间
在区间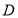 上可被
上可被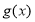 替代,
替代,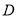 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:①
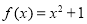 在区间
在区间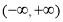 上可被
上可被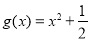 替代;
替代;②
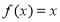 可被
可被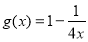 替代的一个“替代区间”为
替代的一个“替代区间”为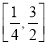 ;
;③
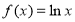 在区间
在区间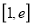 可被
可被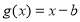 替代,则
替代,则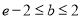 ;
;④
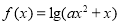 (
(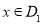 ),
),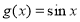 (
(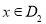 ),则存在实数
),则存在实数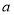 (
(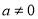 ),使得
),使得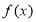 在区间
在区间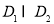 上被
上被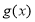 替代; 其中真命题有 .
替代; 其中真命题有 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
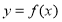 在
在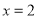 处取得极小值,求
处取得极小值,求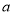 的值;
的值;(2)若
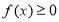 在
在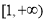 上恒成立,求
上恒成立,求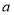 的取值范围;
的取值范围;(3)求证:当
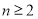 时,
时,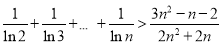 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
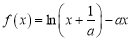 ,其中
,其中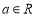 且
且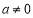 .
.(Ⅰ)讨论
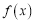 的单调区间;
的单调区间;(Ⅱ)若直线
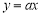 的图象恒在函数
的图象恒在函数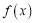 图像的上方,求
图像的上方,求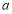 的取值范围;
的取值范围;(Ⅲ)若存在
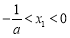 ,
,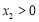 ,使得
,使得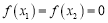 ,求证:
,求证: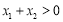 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
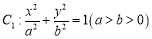 的左、右焦点分别是
的左、右焦点分别是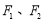 ,下顶点为
,下顶点为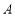 ,线段
,线段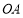 的中点为
的中点为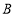 (
(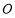 为坐标原点),如图,若抛物线
为坐标原点),如图,若抛物线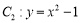 与
与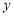 轴的交点为
轴的交点为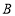 ,且经过
,且经过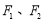 点.
点.
(1)求椭圆
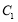 的方程;
的方程;(2)设
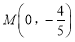 ,
,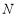 为抛物线
为抛物线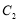 上的一动点,过点
上的一动点,过点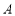 作抛物线
作抛物线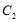 的切线交椭圆
的切线交椭圆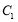 于点
于点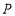 、
、 两点,求
两点,求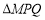 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 :
: 内有一点
内有一点 ,过点
,过点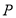 作直线
作直线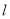 交圆
交圆 于
于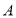 、
、 两点.
两点.(1)当
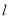 经过圆心
经过圆心 时,求直线
时,求直线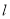 的方程;
的方程;(2)当弦
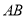 被点
被点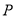 平分时,写出直线
平分时,写出直线 的方程;
的方程;(3)当直线
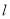 的倾斜角为
的倾斜角为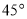 时,求弦
时,求弦 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市随机抽取一年(365天)内100天的空气质量指数
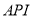 的检测数据,结果统计如下:
的检测数据,结果统计如下: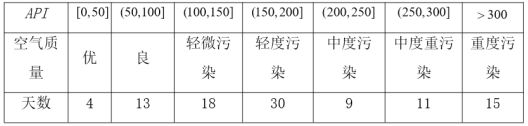
记某企业每天由空气污染造成的经济损失
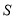 (单位:元),空气质量指数
(单位:元),空气质量指数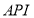 为
为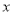 .在区间
.在区间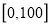 对企业没有造成经济损失;在区间
对企业没有造成经济损失;在区间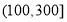 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当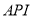 为150时造成的经济损失为500元,当
为150时造成的经济损失为500元,当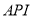 为200时,造成的经济损失为700元);当
为200时,造成的经济损失为700元);当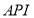 大于300时造成的经济损失为2000元.
大于300时造成的经济损失为2000元.(1)试写出
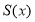 的表达式;
的表达式;(2)试估计在本年内随机抽取一天,该天经济损失
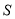 大于200元且不超过600元的概率;
大于200元且不超过600元的概率;(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面
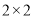 列联表,并判断
列联表,并判断能否有
 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?附:
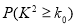
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
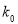
1.32
2.07
2.70
3.74
5.02
6.63
7.87
10.82
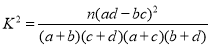
非重度污染
重度污染
合计
供暖季
非供暖季
合计
100
相关试题

