【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)若![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)由![]() ,得
,得![]() ,根据
,根据![]() 是函数
是函数![]() 的极值点,即可求解实数
的极值点,即可求解实数![]() 的值;(II)由
的值;(II)由![]() 在区间
在区间![]() 上单调递增,得
上单调递增,得![]() 在区间
在区间![]() 上恒成立,得到
上恒成立,得到![]() 对区间
对区间![]() 恒成立,设
恒成立,设![]() ,利用导数求解函数
,利用导数求解函数![]() 的最小值,即可求解实数
的最小值,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由![]() ,得
,得![]() ,………………2分
,………………2分
∵![]() 是函数
是函数![]() 的极值点,
的极值点,
∴ ![]() ,解得
,解得![]() ,………4分
,………4分
经检验![]() 为函数,
为函数,![]() 的极值点,(不检验1分扣去)
的极值点,(不检验1分扣去)
所以![]() .……………5分
.……………5分
(Ⅱ)∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴![]() 对区间
对区间![]() 恒成立,………8分
恒成立,………8分
令![]() ,则
,则![]()
∴当![]() 时,
时,![]() ,有
,有![]() ……………12分
……………12分
∴![]() 的取值范围为
的取值范围为![]() …………13分
…………13分
法二:上同,
∴![]() 对区间
对区间![]() 恒成立,………………8分
恒成立,………………8分
令![]() ,
,![]() ,则
,则![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,在
,在![]() 上单调递增函数
上单调递增函数
∴![]() ………………12分
………………12分
∴![]() 的取值范围为
的取值范围为![]() ………………13分
………………13分
法三:∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() 在区间
在区间![]() 上恒成立,………………8分
上恒成立,………………8分
记![]() ,则
,则
![]() 或
或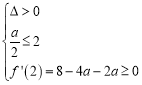
即![]() 或
或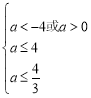
解得![]() ………………12分
………………12分
∴![]() 的取值范围为
的取值范围为![]() ……………13分
……………13分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
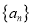 ,
,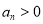 ,其前
,其前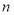 项和
项和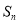 满足
满足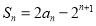 ,其中
,其中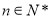 .
.(1)设
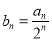 ,证明:数列
,证明:数列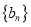 是等差数列;
是等差数列;(2)设
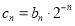 ,
,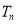 为数列
为数列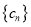 的前
的前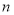 项和,求证:
项和,求证: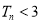 ;
;(3)设
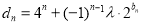 (
(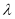 为非零整数,
为非零整数,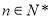 ),试确定
),试确定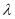 的值,使得对任意
的值,使得对任意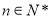 ,都有
,都有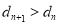 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
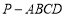 中,底面
中,底面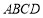 为菱形,
为菱形,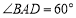 ,
,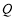 为
为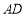 的中点.
的中点.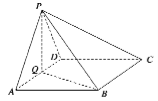
(1)若
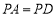 ,求证:
,求证: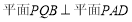 ;
;(2)若
 ,且
,且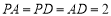 ,点
,点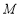 在线段
在线段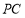 上,试确定点
上,试确定点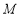 的位置,使二面角
的位置,使二面角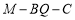 大小为
大小为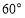 ,并求出
,并求出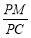 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
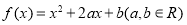 .
.(1)当
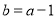 时,求函数
时,求函数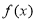 在
在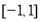 上的最大值
上的最大值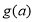 的表达式;
的表达式;(2)当
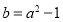 时,讨论函数
时,讨论函数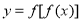 在
在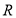 上的零点个数.
上的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】对定义在区间
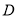 上的函数
上的函数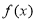 和
和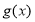 ,如果对任意
,如果对任意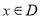 ,都有
,都有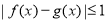 成立,那么称函数
成立,那么称函数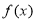 在区间
在区间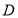 上可被
上可被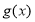 替代,
替代,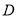 称为“替代区间”.给出以下问题:
称为“替代区间”.给出以下问题:①
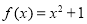 在区间
在区间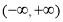 上可被
上可被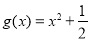 替代;
替代;②
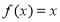 可被
可被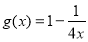 替代的一个“替代区间”为
替代的一个“替代区间”为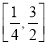 ;
;③
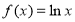 在区间
在区间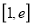 可被
可被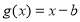 替代,则
替代,则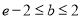 ;
;④
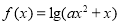 (
(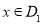 ),
),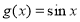 (
(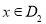 ),则存在实数
),则存在实数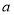 (
(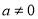 ),使得
),使得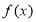 在区间
在区间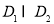 上被
上被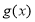 替代; 其中真命题有 .
替代; 其中真命题有 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
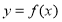 在
在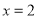 处取得极小值,求
处取得极小值,求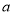 的值;
的值;(2)若
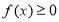 在
在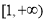 上恒成立,求
上恒成立,求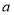 的取值范围;
的取值范围;(3)求证:当
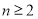 时,
时,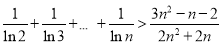 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
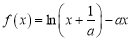 ,其中
,其中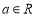 且
且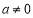 .
.(Ⅰ)讨论
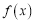 的单调区间;
的单调区间;(Ⅱ)若直线
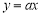 的图象恒在函数
的图象恒在函数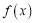 图像的上方,求
图像的上方,求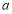 的取值范围;
的取值范围;(Ⅲ)若存在
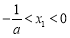 ,
,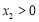 ,使得
,使得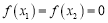 ,求证:
,求证: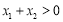 .
.
相关试题

