【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的图象,当
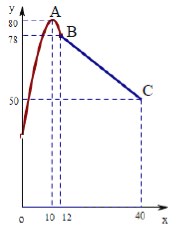
(单位:分钟)之间的关系满足如图所示的图象,当![]() 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点![]() ,过点
,过点![]() ;当
;当![]() 时,图象是线段
时,图象是线段![]() ,其中
,其中![]() .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
参考答案:
【答案】(1)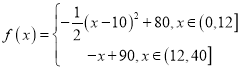 (2)老师在
(2)老师在![]() 时段内安排核心内容,能使得学生学习效果最佳
时段内安排核心内容,能使得学生学习效果最佳
【解析】
试题分析:(1)当![]() 时,设
时,设![]() ,把点
,把点![]() 代入能求出解析式;当
代入能求出解析式;当![]() 时,设
时,设![]() ,把点
,把点![]() 代入能求出解析式.即可得到
代入能求出解析式.即可得到![]() 的函数关系式;
的函数关系式;
(2)由(1)的解析式,结合题设条件,列出不等式组,能求出老师就在什么时段内安排核心内容,能使得学生学习效果最佳
试题解析:(1)当![]() 时,设
时,设![]()
过点![]() 代入得,
代入得,![]() ,
,
则![]()
当![]() 时,设
时,设![]() ,过点
,过点![]() 得
得
![]() ,即
,即![]()
则得函数关系式为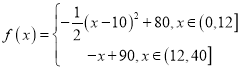
(2)由题意得, 或
或![]()
得![]() 或
或![]() ,即
,即![]()
则老师在![]() 时段内安排核心内容,能使得学生学习效果最佳.
时段内安排核心内容,能使得学生学习效果最佳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
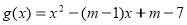 .
.(1)若函数
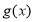 在
在 上具有单调性,求实数
上具有单调性,求实数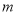 的取值范围;
的取值范围;(2)若在区间
 上,函数
上,函数 的图象恒在
的图象恒在 图象上方,求实数
图象上方,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
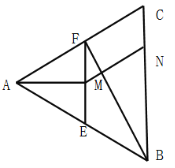
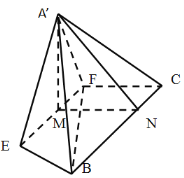
查看答案和解析>>【题目】如图,已知等边
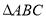 中,
中,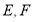 分别为
分别为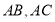 边的中点,
边的中点,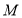 为
为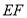 的中点,
的中点,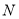 为
为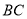 边上一点,且
边上一点,且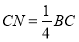 ,将
,将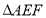 沿
沿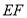 折到
折到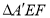 的位置,使平面
的位置,使平面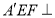 平面
平面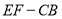 .
.
(I)求证:平面
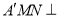 平面
平面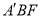 ;
;(II)求二面角
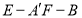 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数
 与听课时间
与听课时间 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点 ,过点
,过点 ;当
;当 时,图象是线段
时,图象是线段 ,其中
,其中 .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求
 的函数关系式;
的函数关系式;(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
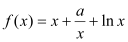 ,
,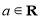 .
.(Ⅰ)若
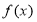 在
在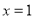 处取得极值,求
处取得极值,求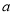 的值;
的值;(Ⅱ)若
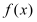 在区间
在区间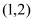 上单调递增, 求
上单调递增, 求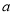 的取值范围;
的取值范围;(Ⅲ)讨论函数
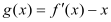 的零点个数.
的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
 的函数
的函数 是奇函数.
是奇函数.(1)求
 的值;
的值;(2)判断函数
 的单调性,并用定义证明;
的单调性,并用定义证明;(3)当
 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国的烟火名目繁多,花色品种繁杂.其中“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,通过研究,发现该型烟花爆裂时距地面的高度
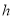 (单位:米)与时间
(单位:米)与时间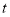 (单位:秒)存在函数关系,并得到相关数据如下表:
(单位:秒)存在函数关系,并得到相关数据如下表:
(1)根据上表数据,从下列函数中,选取一个函数描述该型烟花爆裂时距地面的高度
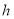 与时间
与时间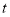 的变化关系:
的变化关系: ,确定此函数解析式,并简单说明理由;
,确定此函数解析式,并简单说明理由; (2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求出此时烟花距地面的高度.
相关试题

