【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上具有单调性,求实数
上具有单调性,求实数![]() 的取值范围;
的取值范围;
(2)若在区间![]() 上,函数
上,函数![]() 的图象恒在
的图象恒在![]() 图象上方,求实数
图象上方,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)由函数解析式可求得函数对称轴,从而得到函数的单调区间,得到区间![]() 与单调区间的关系,从而求得m的取值范围;(2)中由函数图像的上下方位置关系可得到函数值的大小关系,从而得到不等式恒成立问题,将不等式转化为函数,通过考察函数的最值得到m需满足的条件,从而求解其取值范围
与单调区间的关系,从而求得m的取值范围;(2)中由函数图像的上下方位置关系可得到函数值的大小关系,从而得到不等式恒成立问题,将不等式转化为函数,通过考察函数的最值得到m需满足的条件,从而求解其取值范围
试题解析:(1)对称轴![]() ,且图象开口向上.
,且图象开口向上.
若函数![]() 在
在![]() 上具有单调性,则满足
上具有单调性,则满足![]()
解得:![]() ---------------------4分
---------------------4分
(2)若在区间![]() 上,函数
上,函数![]() 的图象恒在
的图象恒在![]() 图象上方,则只需:
图象上方,则只需:
![]() 在区间
在区间![]() 恒成立
恒成立
即![]() 对任意
对任意![]() 恒成立---------------6分
恒成立---------------6分
设![]() 其图象的对称轴为直线
其图象的对称轴为直线![]() ,且图象开口向上
,且图象开口向上
①当![]() 时,h(x)在[-1,1]上是减函数,所以
时,h(x)在[-1,1]上是减函数,所以![]()
所以,![]()
②当![]() 即
即![]() ,函数h(x)在顶点处取得最小值,即
,函数h(x)在顶点处取得最小值,即
![]() 解得:
解得:![]()
③当![]() 时,h(x)在[-1,1]上是增函数,所以,
时,h(x)在[-1,1]上是增函数,所以,
![]()
综上所述:![]() -----------------------------12分
-----------------------------12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
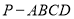 中,
中,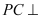 底面
底面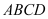 ,底面
,底面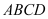 是矩形,
是矩形,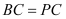 ,
,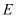 是
是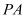 的中点.
的中点.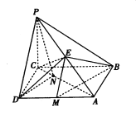
(1)求证:
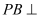 平面
平面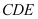 ;
;(2)已知点
 是
是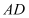 的中点,点
的中点,点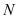 是
是 上一点,且平面
上一点,且平面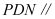 平面
平面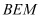 .若
.若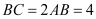 ,求点
,求点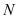 到平面
到平面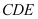 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】重庆一中开展了丰富多彩的社团文化活动,甲,乙,丙三位同学在被问到是否参加过街舞社,动漫社,器乐社这三个社团时,
甲说:我参加过的社团比乙多,但没有参加过动漫社;
乙说:我没有参加过器乐社;
丙说:我们三个人都参加过同一个社团,由此判断乙参加过的社团为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
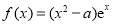 ,
, .
.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)若在区间
 上存在不相等的实数
上存在不相等的实数 ,使
,使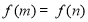 成立,求
成立,求 的取值范围;
的取值范围;(Ⅲ)若函数
 有两个不同的极值点
有两个不同的极值点 ,
, ,求证:
,求证: .
. -
科目: 来源: 题型:
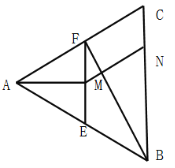
查看答案和解析>>【题目】如图,已知等边
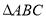 中,
中,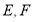 分别为
分别为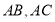 边的中点,
边的中点,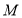 为
为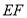 的中点,
的中点,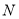 为
为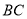 边上一点,且
边上一点,且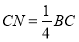 ,将
,将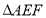 沿
沿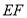 折到
折到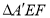 的位置,使平面
的位置,使平面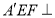 平面
平面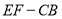 .
.
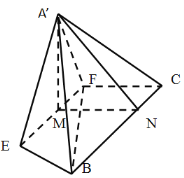
(I)求证:平面
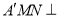 平面
平面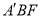 ;
;(II)求二面角
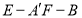 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数
 与听课时间
与听课时间 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点 ,过点
,过点 ;当
;当 时,图象是线段
时,图象是线段 ,其中
,其中 .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求
 的函数关系式;
的函数关系式;(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数
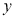 与听课时间
与听课时间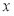 (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当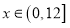 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点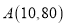 ,过点
,过点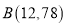 ;当
;当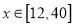 时,图象是线段
时,图象是线段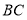 ,其中
,其中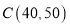 .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.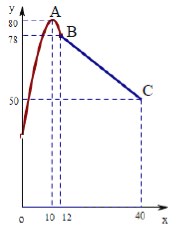
(1)试求
 的函数关系式;
的函数关系式;(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
相关试题

