【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为![]() ,且点
,且点![]() 在该椭圆上。
在该椭圆上。
(I)求椭圆C的方程;
(II)过椭圆C的左焦点![]() 的直线l与椭圆C相交于
的直线l与椭圆C相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)设出椭圆的标准方程,根据离心率求得a和c关系,进而根据a2=b2+c2,求得a和b的关系,把点C坐标代入椭圆方程求得a,进而求得b,则椭圆方程可得.
(2)先看当l与x轴垂直时,可求得A,B的坐标,进而求得三角形AOB的坐标,不符合题意;再看直线l斜率存在时,设出直线方程,与椭圆方程联立消去y,设A(x1,y1),B(x2,y2),进而求得x1+x2和x1x2的表达式,进而表示出|AB|,进而求得圆的半径后表示出三角形AOB的面积,求得k,进而求得圆的半径,则圆的方程可得.
解析:
(1)设椭圆C的方程为![]() ,(
,( ![]() ),由题意可得
),由题意可得![]()
又![]() ,所以
,所以![]()
因为椭圆C经过(1, ![]() ),代入椭圆方程有
),代入椭圆方程有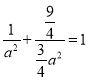
解得![]()
所以c=1, ![]() 故椭圆C的方程为
故椭圆C的方程为![]()
(II)当直线![]() 轴时,计算得到:
轴时,计算得到: ![]() ,
, ![]()
![]() ,不符合题意
,不符合题意
当直线l与x轴不垂直时,设直线l的方程为: ![]() ,
, ![]()
由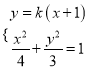 消去y,得
消去y,得![]()
显然![]() 成立,设
成立,设![]() ,
, ![]()
则![]() ,
, ![]() 又
又![]()
![]()
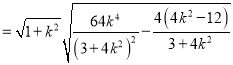
即![]()
又圆O的半径![]()
所以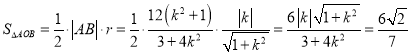
化简,得![]() ,即
,即![]()
解得![]() ,
, ![]() (舍)
(舍)
所以, 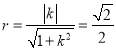 ,故圆O的方程为:
,故圆O的方程为: ![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m,n为两条不同的直线,
 ,
, 为两个不同的平面,则下列命题中正确的有
为两个不同的平面,则下列命题中正确的有

 ,
, ,
, ,
,
 ,
,
 ,
, ,
,
 ,
,
A. 0个 B. 1个 C. 2个 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点
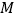 在正视图上的对应点为
在正视图上的对应点为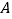 ,圆柱表面上的点
,圆柱表面上的点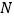 在左视图上的对应点为
在左视图上的对应点为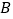 ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从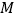 到
到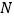 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.
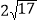 B.
B. 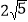 C.
C. 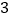 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
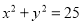 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且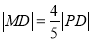 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
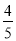 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.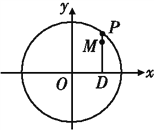
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点为F,过椭圆C中心的弦PQ长为2,且∠PFQ=90°,△PQF的面积为1.
的右焦点为F,过椭圆C中心的弦PQ长为2,且∠PFQ=90°,△PQF的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A1、A2分别为椭圆C的左、右顶点,S为直线 上一动点,直线A1S交椭圆C于点M,直线A2S交椭圆于点N,设S1、S2分别为△A1SA2、△MSN的面积,求
上一动点,直线A1S交椭圆C于点M,直线A2S交椭圆于点N,设S1、S2分别为△A1SA2、△MSN的面积,求  的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 成立,求实数a的取值范围.
成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】四面体
 中,
中, ,
, ,
, ,则此四面体外接球的表面积为
,则此四面体外接球的表面积为 
A.
 B.
B.  C.
C.  D.
D. 
相关试题

