搜索
【题目】某圆柱的高为2，底面周长为16，其三视图如图所示，圆柱表面上的点
在正视图上的对应点为
，圆柱表面上的点
在左视图上的对应点为
，则在此圆柱侧面上，从到的路径中，最短路径的长度为（ ）
A. 
B. 
C. 
D. 2
参考答案：
【答案】B
【解析】
分析：首先根据题中所给的三视图，得到点M和点N在圆柱上所处的位置，点M在上底面上，点N在下底面上，并且将圆柱的侧面展开图平铺，点M、N在其四分之一的矩形的对角线的端点处，根据平面上两点间直线段最短，利用勾股定理，求得结果.
详解：根据圆柱的三视图以及其本身的特征，
可以确定点M和点N分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处，
所以所求的最短路径的长度为
，故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】椭圆
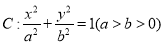的左右焦点分别为F1，F2，离心率为
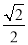，过点F1且垂直于x轴的直线被椭圆截得的弦长为
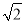，直线l：y=kx+m与椭圆交于不同的A，B两点．（Ⅰ）求椭圆C的方程；
（Ⅱ）若在椭圆C上存在点Q满足：
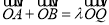（O为坐标原点）．求实数λ的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知m＞0，
， 
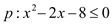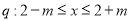. (1) 若p是q的充分不必要条件，求实数m的取值范围；
(2) 若m=5，“
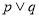”为真命题，“
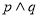”为假命题，求实数x的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知m，n为两条不同的直线，
，
为两个不同的平面，则下列命题中正确的有
，
，
，
，
，
，
，
A. 0个 B. 1个 C. 2个 D. 3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,设P是圆
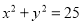上的动点,点D是P在x轴上的投影，M为线段PD上一点,且
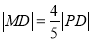，(1)当P在圆上运动时,求点M的轨迹C的方程；
(2)求过点(3,0)且斜率为
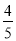的直线被轨迹C所截线段的长度.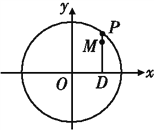
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C的对称中心为原点O，焦点在x轴上，离心率为
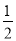，且点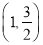
在该椭圆上。（I）求椭圆C的方程；
（II）过椭圆C的左焦点
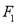的直线l与椭圆C相交于
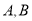两点，若
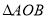的面积为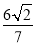
，求圆心在原点O且与直线l相切的圆的方程。 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆
的右焦点为F，过椭圆C中心的弦PQ长为2，且∠PFQ=90°，△PQF的面积为1．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设A1、A2分别为椭圆C的左、右顶点，S为直线
上一动点，直线A1S交椭圆C于点M，直线A2S交椭圆于点N，设S1、S2分别为△A1SA2、△MSN的面积，求 
的最大值．
相关试题
