【题目】四面体 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,则此四面体外接球的表面积为
,则此四面体外接球的表面积为 ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
分析:由△BCD中,CB=DB=2,∠CBD=60°,可知△BCD是等边三角形,∠ABC=∠ABD=60°,可得AD=AC=![]() ,求出底面△BCD的外接圆半径r=
,求出底面△BCD的外接圆半径r=![]() .利用球心到圆心构造直角三角形即可求解外接球R.
.利用球心到圆心构造直角三角形即可求解外接球R.
详解:
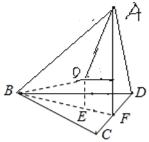
由题意,△BCD中,CB=DB=2,∠CBD=60°,
可知△BCD是等边三角形,BF=![]()
∴△BCD的外接圆半径r=![]() =BE,FE=
=BE,FE=![]()
∵∠ABC=∠ABD=60°,可得AD=AC=![]() ,
,
可得AF=![]()
∴AF⊥FB
∴AF⊥BCD,
∴四面体A﹣BCD高为AF=![]() .
.
设:外接球R,O为球心,OE=m
可得:r2+m2=R2……①,
(![]() )2+EF2=R2……②
)2+EF2=R2……②
由①②解得:R=![]() .
.
四面体外接球的表面积:S=4πR2=![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为
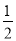 ,且点
,且点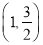 在该椭圆上。
在该椭圆上。(I)求椭圆C的方程;
(II)过椭圆C的左焦点
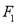 的直线l与椭圆C相交于
的直线l与椭圆C相交于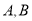 两点,若
两点,若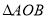 的面积为
的面积为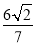 ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点为F,过椭圆C中心的弦PQ长为2,且∠PFQ=90°,△PQF的面积为1.
的右焦点为F,过椭圆C中心的弦PQ长为2,且∠PFQ=90°,△PQF的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A1、A2分别为椭圆C的左、右顶点,S为直线 上一动点,直线A1S交椭圆C于点M,直线A2S交椭圆于点N,设S1、S2分别为△A1SA2、△MSN的面积,求
上一动点,直线A1S交椭圆C于点M,直线A2S交椭圆于点N,设S1、S2分别为△A1SA2、△MSN的面积,求  的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 成立,求实数a的取值范围.
成立,求实数a的取值范围. -
科目: 来源: 题型:
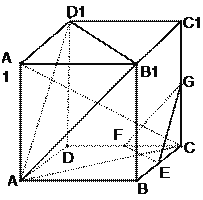
查看答案和解析>>【题目】如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线
 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:
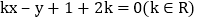
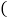 1
1 证明直线l经过定点并求此点的坐标;
证明直线l经过定点并求此点的坐标; 2
2 若直线l不经过第四象限,求k的取值范围;
若直线l不经过第四象限,求k的取值范围; 3
3 若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设
若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设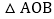 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1,
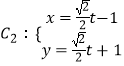 (t为参数).
(t为参数).
(Ⅰ)求曲线C1上的点到曲线C2距离的最小值;
(Ⅱ)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的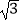 倍,得到曲线
倍,得到曲线 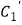 .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 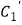 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|.
相关试题

