【题目】已知椭圆 ![]() 的右焦点为F,过椭圆C中心的弦PQ长为2,且∠PFQ=90°,△PQF的面积为1.
的右焦点为F,过椭圆C中心的弦PQ长为2,且∠PFQ=90°,△PQF的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A1、A2分别为椭圆C的左、右顶点,S为直线 ![]() 上一动点,直线A1S交椭圆C于点M,直线A2S交椭圆于点N,设S1、S2分别为△A1SA2、△MSN的面积,求
上一动点,直线A1S交椭圆C于点M,直线A2S交椭圆于点N,设S1、S2分别为△A1SA2、△MSN的面积,求 ![]() 的最大值.
的最大值.
参考答案:
【答案】解:(Ⅰ)弦PQ过椭圆中心,且∠PFQ=90°,则c=丨OF丨= ![]() 丨PQ丨=1,
丨PQ丨=1,
不妨设P(x0 , y0)(x0 , y0>0),
∴,△PQF的面积= ![]() ×丨OF丨×2y0=y0=1,则x0=1,b=1,
×丨OF丨×2y0=y0=1,则x0=1,b=1,
a2=b2+c2=2,
∴椭圆方程为 ![]() +y2=1;
+y2=1;
(Ⅱ)设S(2 ![]() ,t),直线A1S:x=
,t),直线A1S:x= ![]() y﹣
y﹣ ![]() ,则
,则 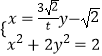 ,
,
整理( ![]() +2)y2﹣
+2)y2﹣ ![]() y=0,解得y1=
y=0,解得y1= ![]() ,
,
同理,设直线A2S:x= ![]() y+
y+ ![]() ,
, 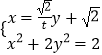
得( ![]() +2)y2+
+2)y2+ ![]() y=0,解得y1=﹣
y=0,解得y1=﹣ ![]() ,
,
则 ![]() =丨
=丨 ![]() ×
× ![]() 丨
丨
≤ 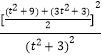 ×
× ![]() =
= ![]() ,
,
当且仅当t2+9=3t2+3,即t=± ![]() 时取“=”
时取“=”
【解析】(Ⅰ)由c=丨OF丨= ![]() 丨PQ丨=1,根据三角形的面积公式,即可求得b的值,a2=b2+c2=2,即可求得椭圆方程;(Ⅱ)设S点坐标,求直线A1S及A2S代入椭圆方程,求得M和N点坐标,根据三角形的面积公式及基本不等式的性质,即可求得
丨PQ丨=1,根据三角形的面积公式,即可求得b的值,a2=b2+c2=2,即可求得椭圆方程;(Ⅱ)设S点坐标,求直线A1S及A2S代入椭圆方程,求得M和N点坐标,根据三角形的面积公式及基本不等式的性质,即可求得 ![]() 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点
 在正视图上的对应点为
在正视图上的对应点为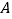 ,圆柱表面上的点
,圆柱表面上的点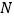 在左视图上的对应点为
在左视图上的对应点为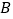 ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从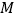 到
到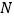 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.
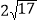 B.
B. 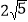 C.
C. 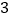 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
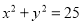 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且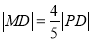 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
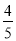 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.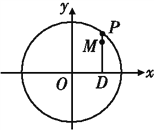
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为
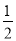 ,且点
,且点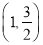 在该椭圆上。
在该椭圆上。(I)求椭圆C的方程;
(II)过椭圆C的左焦点
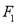 的直线l与椭圆C相交于
的直线l与椭圆C相交于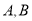 两点,若
两点,若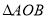 的面积为
的面积为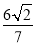 ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 成立,求实数a的取值范围.
成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】四面体
 中,
中, ,
, ,
, ,则此四面体外接球的表面积为
,则此四面体外接球的表面积为 
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
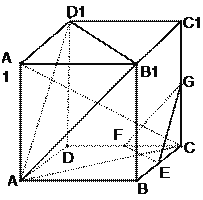
查看答案和解析>>【题目】如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线
 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .
相关试题

