【题目】对于函数y=f(x),如果存在区间[m,n],同时满足下列条件:
1)f(x)在[m,n]上是单调的;
2)当定义域是[m,n]时,f(x)的值域也是[m,n],则称[m,n]是该函数的“和谐区间”.若函数f(x)= ![]() ﹣
﹣ ![]() (a>0)存在“和谐区间”,则实数a的取值范围是 .
(a>0)存在“和谐区间”,则实数a的取值范围是 .
参考答案:
【答案】0<a<1
【解析】解:由题意可得函数 ![]() 在区间[m,n]是单调递增的,
在区间[m,n]是单调递增的,
∴[m,n](﹣∞,0)或[m,n](0,+∞),则f(m)=m,f(n)=n,
故m、n是方程f(x)=x的两个同号的不等实数根,
即 ![]() ,
,
即方程ax2﹣(a+1)x+a=0有两个同号的实数根,
∵mn= ![]() ,
,
故只需△=(a+1)2﹣4a2>0,解得 ![]() <a<1,
<a<1,
∵a>0,
∴0<a<1.
所以答案是:0<a<1.
【考点精析】通过灵活运用函数的值域和函数单调性的判断方法,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:
①“等边三角形的三个内角均为60°”的逆命题;
②“若k>0,则方程x2+2x﹣k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题;
④“若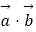 =
= 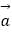
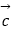 ,则
,则 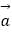 ⊥
⊥ 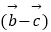 ”的否命题,
”的否命题,
其中真命题的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=a
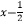 (a>0且a≠1),若f(lga)=
(a>0且a≠1),若f(lga)= 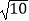 ,则a= .
,则a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
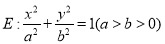 的左、右焦点分别为
的左、右焦点分别为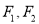 ,左、右顶点分别为
,左、右顶点分别为 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为 .设点
.设点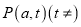 ,连接PA交椭圆于点C.
,连接PA交椭圆于点C.(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求t的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,
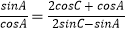 是角A、B、C成等差数列的( )
是角A、B、C成等差数列的( )
A.充分非必要条件
B.充要条件
C.充分不必要条件
D.必要不充分条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Sn是等差数列{an}的前n项和,且S6>S7>S5 , 给出下列五个命题:①d<1;②S11>0;③S12<0;④数列{Sn}中的最大项为S11;⑤|a6|>|a7|.其中正确命题有 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
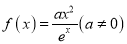 ,
, 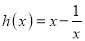 .
.(I)求函数
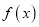 的单调区间;
的单调区间;(II)设
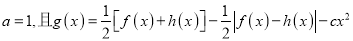 ,已知函数
,已知函数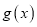 在
在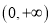 上是增函数.
上是增函数.(1)研究函数
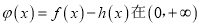 上零点的个数;
上零点的个数;(ii)求实数c的取值范围.
相关试题

