【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点, ![]() 轴正半轴为极轴建立坐标系,直线
轴正半轴为极轴建立坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(Ⅱ)曲线![]() 交
交![]() 轴于
轴于![]() 两点,且点
两点,且点![]() ,
, ![]() 为直线
为直线![]() 上的动点,求
上的动点,求![]() 周长的最小值.
周长的最小值.
参考答案:
【答案】(Ⅰ)![]() ,
, ![]() ;Ⅱ)
;Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由极直互化公式可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() , 消去参数
, 消去参数![]()
得C得普通方程为![]()
(Ⅱ)求点A关于直线l的对称点为M(a,b),由题易知当P为MB与直线l的交点时![]() 周长最小.
周长最小.
试题解析:(Ⅰ)由直线![]() 的极坐标方程,得
的极坐标方程,得![]()
即![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
由曲线C的参数方程得C得普通方程为![]()
(Ⅱ)由(Ⅰ)知曲线C表示圆心![]() ,半径
,半径![]() 的圆,令
的圆,令![]() 得
得![]()
A的坐标为![]() ,B的坐标为
,B的坐标为![]()
设A关于直线l的对称点为M(a,b),则有
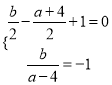 解得
解得![]() ,即点M(1,3
,即点M(1,3
由题易知当P为MB与直线l的交点时![]() 周长最小,最小值为
周长最小,最小值为![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂某种产品的年固定成本为250万元,每生产
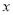 千件,需另投入成本为
千件,需另投入成本为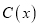 ,当年产量不足80千件时,
,当年产量不足80千件时, 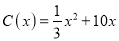 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, 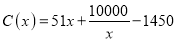 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(Ⅰ)写出年利润
 (万元)关于年产量
(万元)关于年产量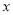 (千件)的函数解析式;
(千件)的函数解析式;(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x+
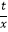 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, 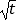 ]上是减函数,在[
]上是减函数,在[ 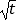 ,+∞)上是增函数.
,+∞)上是增函数.
(1)若f(x)=x+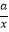 ,函数在(0,a]上的最小值为4,求a的值;
,函数在(0,a]上的最小值为4,求a的值;
(2)对于(1)中的函数在区间A上的值域是[4,5],求区间长度最大的A(注:区间长度=区间的右端点﹣区间的左断点);
(3)若(1)中函数的定义域是[2,+∞)解不等式f(a2﹣a)≥f(2a+4). -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式
实施地点
大雨
中雨
小雨
模拟实验次数
A
甲
2次
6次
4次
12次
B
乙
3次
6次
3次
12次
C
丙
2次
2次
8次
12次
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量
 ,求
,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
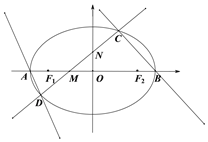
查看答案和解析>>【题目】如图,椭圆E的左右顶点分别为A、B,左右焦点分别为
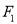 、
、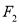 ,
,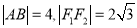 ,直线
,直线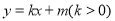 交椭圆于C、D两点,与线段
交椭圆于C、D两点,与线段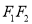 及椭圆短轴分别交于
及椭圆短轴分别交于 两点(
两点(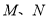 不重合),且
不重合),且 .
.
(Ⅰ)求椭圆E的离心率;
(Ⅱ)若
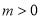 ,设直线
,设直线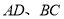 的斜率分别为
的斜率分别为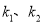 ,求
,求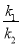 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
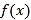 在区间
在区间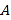 上,
上, 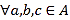 ,
, 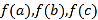 ,
,  ,
, 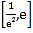 ,
, 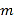 ,
, 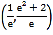 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数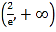 为“三角形函数”.已知函数
为“三角形函数”.已知函数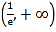 在区间
在区间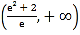 上是“三角形函数”,则实数
上是“三角形函数”,则实数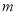 的取值范围为( )
的取值范围为( )A.
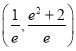 B.
B. 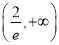
C.
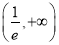 D.
D. 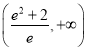
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,是偶函数,且在区间(0,1)上为增函数的是( )
A.y=|x|
B.y=1﹣x
C.y=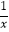
D.y=﹣x2+4
相关试题

