【题目】已知函数f(x)= ![]() 的图象过点A(0,
的图象过点A(0, ![]() ),B(3,3)
),B(3,3)
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(2,+∞)上的单调性,并用单调性的定义加以证明;
(3)若m,n∈(2,+∞)且函数f(x)在[m,n]上的值域为[1,3],求m+n的值.
参考答案:
【答案】
(1)解:函数f(x)= ![]() 的图象过点A(0,
的图象过点A(0, ![]() ),B(3,3),
),B(3,3),
∴ 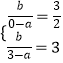 ,解得:
,解得: ![]()
∴f(x)= ![]()
(2)解:函数f(x)在(2,+∞)上单调递减,
证明:任取x2>x1>2,
则f(x1)﹣f(x2)= ![]()
∵x2>x1>2,
∴x2﹣x1>0,x1﹣2>0,x2﹣2>0,
∴ ![]() >0,得f(x1)﹣f(x2)>0,
>0,得f(x1)﹣f(x2)>0,
∴f(x1)>f(x2),
函数f(x)在(2,+∞)上是单调递减函数
(3)解:∵m,n∈(2,+∞),
∴函数f(x)在[m,n]上单调递减,
∴f(m)=3,f(n)=1
∴ ![]() =3,
=3, ![]() =1,
=1,
∴m=3,n=5,
∴m+n=8
【解析】(1)将A、B的坐标代入函数的解析式,求出a,b的值即可;(2)根据函数单调性的定义证明即可;(3)根据函数的单调性得到关于m、n的方程,求出m、n的值,从而求出m+n的值即可.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ,1)上是减函数,求a的取值范围.
,1)上是减函数,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为自然对数的底数)
为自然对数的底数)(Ⅰ)试讨论函数
 的零点个数;
的零点个数;(Ⅱ)证明:当
 且
且 时,总有
时,总有
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足(an+1﹣1)(an﹣1)=
 (an﹣an+1),a1=2,若bn=
(an﹣an+1),a1=2,若bn=  .
.
(1)证明:数列{bn}是等差数列;
(2)令cn= ,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥
,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥  (n∈N*).
(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
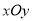 中,点
中,点 ,圆
,圆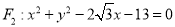 ,以动点
,以动点 为圆心的圆经过点
为圆心的圆经过点 ,且圆
,且圆 与圆
与圆 内切.
内切.(Ⅰ)求动点
 的轨迹
的轨迹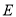 的方程;
的方程;(Ⅱ)若直线
 过点
过点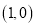 ,且与曲线
,且与曲线 交于
交于 两点,则在
两点,则在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 轴平分
轴平分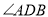 ?若存在,求出
?若存在,求出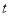 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在梯形
 中,
中, 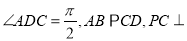 平面
平面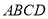 ,且
,且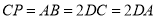 ,点
,点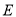 在
在 上,且
上,且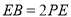 .
. 
(Ⅰ)求证:
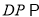 平面
平面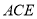 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣a)2lnx(a为常数).
(1)若f(x)在(1,f(1))处的切线与直线2x+2y﹣3=0垂直.
(ⅰ)求实数a的值;
(ⅱ)若a非正,比较f(x)与x(x﹣1)的大小;
(2)如果0<a<1,判断f(x)在(a,1)上是否有极值,若有极值是极大值还是极小值?若无极值,请说明理由.
相关试题

