【题目】已知函数f(x)=(x﹣a)2lnx(a为常数).
(1)若f(x)在(1,f(1))处的切线与直线2x+2y﹣3=0垂直.
(ⅰ)求实数a的值;
(ⅱ)若a非正,比较f(x)与x(x﹣1)的大小;
(2)如果0<a<1,判断f(x)在(a,1)上是否有极值,若有极值是极大值还是极小值?若无极值,请说明理由.
参考答案:
【答案】
(1)解:(ⅰ)f(x)定义域是(0,+∞),f′(x)=(x﹣a)(2lnx+ ![]() ),
),
∵直线2x+2y﹣3=0的斜率为:k=﹣1,
∴f(x)在(1,f(1))处的切线的斜率﹣ ![]() =1,
=1,
即f′(1)=(1﹣a)(2ln1+ ![]() )=(1﹣a)2=1,
)=(1﹣a)2=1,
∴a=0或a=2;
(ⅱ)由(ⅰ)知,a=0,∴f(x)=x2lnx,
∵x2lnx﹣x(x﹣1)=x(xlnx﹣x+1),
∴令g(x)=xlnx﹣x+1,g′(x)=lnx,
当x>1时,g′(x)>0,当0<x<1时,g′(x)<0,
∴g(x)在(0,1)单调递减,在(1,+∞)单调递增,
g(x)min=g(1)=0,∴g(x)≥0恒成立,
即f(x)≥x(x﹣1);
(2)解:f′(x)=(x﹣a)(2lnx+ ![]() ),
),
令F(x)=2lnx+1﹣ ![]() ,F′(x)=
,F′(x)= ![]() >0,
>0,
∴F(x)在(a,1)上单调递增,又F(1)=1﹣a>0,F(a)=2lna<0,
所以在(a,1)上必存在x0,使F(x0)=0,
又x﹣a>0,∴当x∈(a,x0),f′(x)<0,x∈(x0,1),f′(x)>0,
∴f(x)在(a,x0)单调递减,在(x0,1)单调递增,
∴x=x0是f(x)的极值点,且为极小值.
【解析】(1)(i)求出f(x)的导数,根据切线的斜率是f′(1)=﹣ ![]() =1,解出a的值即可;(ii)求出f(x)的表达式,作差,得到x2lnx﹣x(x﹣1)=x(xlnx﹣x+1),令g(x)=xlnx﹣x+1,根据函数的单调性求出g(x)的最小值g(1)=0,得到g(x)≥0恒成立,从而求出f(x)与x(x﹣1)的大小即可;(2)求出f′(x)=(x﹣a)(2lnx+
=1,解出a的值即可;(ii)求出f(x)的表达式,作差,得到x2lnx﹣x(x﹣1)=x(xlnx﹣x+1),令g(x)=xlnx﹣x+1,根据函数的单调性求出g(x)的最小值g(1)=0,得到g(x)≥0恒成立,从而求出f(x)与x(x﹣1)的大小即可;(2)求出f′(x)=(x﹣a)(2lnx+ ![]() ),令F(x)=2lnx+1﹣
),令F(x)=2lnx+1﹣ ![]() ,求出F(x)的导数,根据函数的单调性求出函数的极值即可.
,求出F(x)的导数,根据函数的单调性求出函数的极值即可.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
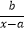 的图象过点A(0,
的图象过点A(0,  ),B(3,3)
),B(3,3)
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(2,+∞)上的单调性,并用单调性的定义加以证明;
(3)若m,n∈(2,+∞)且函数f(x)在[m,n]上的值域为[1,3],求m+n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
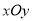 中,点
中,点 ,圆
,圆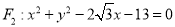 ,以动点
,以动点 为圆心的圆经过点
为圆心的圆经过点 ,且圆
,且圆 与圆
与圆 内切.
内切.(Ⅰ)求动点
 的轨迹
的轨迹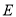 的方程;
的方程;(Ⅱ)若直线
 过点
过点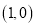 ,且与曲线
,且与曲线 交于
交于 两点,则在
两点,则在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 轴平分
轴平分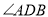 ?若存在,求出
?若存在,求出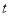 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在梯形
 中,
中, 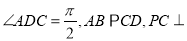 平面
平面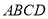 ,且
,且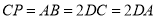 ,点
,点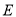 在
在 上,且
上,且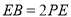 .
. 
(Ⅰ)求证:
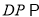 平面
平面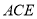 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx﹣ax2有两个极值点,则实数a的取值范围为( )
A.(﹣∞,0)
B.(0,+∞)
C.
D.(0,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线

(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=
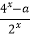 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a+b的值.
(2)若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围.
相关试题

