【题目】已知数列{an}满足(an+1﹣1)(an﹣1)= ![]() (an﹣an+1),a1=2,若bn=
(an﹣an+1),a1=2,若bn= ![]() .
.
(1)证明:数列{bn}是等差数列;
(2)令cn= ![]() ,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥
,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥ ![]() (n∈N*).
(n∈N*).
参考答案:
【答案】
(1)证明:由(an+1﹣1)(an﹣1)= ![]() (an﹣an+1)得
(an﹣an+1)得 ![]() ﹣
﹣ ![]() =2,
=2,
即bn+1﹣bn=2,
∴{bn}是首项为b1= ![]() =1,公差为2的等差数列.
=1,公差为2的等差数列.
(2)解:由(1)知,bn=1+2(n﹣1)=2n﹣1,cn= ![]() =
= ![]() ,
,
①当n=1时,则有T1=1有T1≥ ![]() =1成立;
=1成立;
②假设当n=k时,不等式成立,即Tk≥ ![]() 成立,
成立,
则当n=k+1时,Tk+1=Tk+ck+1= ![]() ≥
≥ ![]() +
+ ![]() ,
,
欲证 ![]() +
+ ![]() ≥
≥ ![]() ,
,
只须证 ![]() +1≥k+1,
+1≥k+1,
即证 ![]() ≥k,即证
≥k,即证 ![]() ≥
≥ ![]() ,即证1≥0,而此式成立
,即证1≥0,而此式成立
故当n=k+1时,不等式也成立.
故有Tn≥ ![]() (n∈N*).
(n∈N*).
【解析】(1)由(an+1﹣1)(an﹣1)= ![]() (an﹣an+1)得
(an﹣an+1)得 ![]() ﹣
﹣ ![]() =2,继而得到{bn}是首项为b1=
=2,继而得到{bn}是首项为b1= ![]() =1,公差为2的等差数列.(2)由数学归纳法和分析法即可证明.
=1,公差为2的等差数列.(2)由数学归纳法和分析法即可证明.
【考点精析】利用等差关系的确定和数学归纳法的定义对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数学归纳法是证明关于正整数n的命题的一种方法.
)那么这个数列就叫做等差数列;数学归纳法是证明关于正整数n的命题的一种方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前n项和为Sn , 公差d≠0,且S3+S5=50,a1 , a4 , a13成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 +
+  +…+
+…+  =an﹣1(n∈N*),求数列{nbn}的前n项和Tn .
=an﹣1(n∈N*),求数列{nbn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ,1)上是减函数,求a的取值范围.
,1)上是减函数,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为自然对数的底数)
为自然对数的底数)(Ⅰ)试讨论函数
 的零点个数;
的零点个数;(Ⅱ)证明:当
 且
且 时,总有
时,总有
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
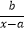 的图象过点A(0,
的图象过点A(0,  ),B(3,3)
),B(3,3)
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(2,+∞)上的单调性,并用单调性的定义加以证明;
(3)若m,n∈(2,+∞)且函数f(x)在[m,n]上的值域为[1,3],求m+n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
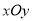 中,点
中,点 ,圆
,圆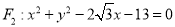 ,以动点
,以动点 为圆心的圆经过点
为圆心的圆经过点 ,且圆
,且圆 与圆
与圆 内切.
内切.(Ⅰ)求动点
 的轨迹
的轨迹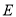 的方程;
的方程;(Ⅱ)若直线
 过点
过点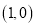 ,且与曲线
,且与曲线 交于
交于 两点,则在
两点,则在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 轴平分
轴平分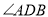 ?若存在,求出
?若存在,求出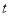 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在梯形
 中,
中, 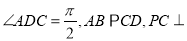 平面
平面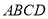 ,且
,且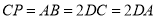 ,点
,点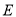 在
在 上,且
上,且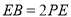 .
. 
(Ⅰ)求证:
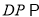 平面
平面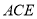 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.
相关试题

