【题目】已知函数![]() (
(![]() 为自然对数的底数)
为自然对数的底数)
(Ⅰ)试讨论函数![]() 的零点个数;
的零点个数;
(Ⅱ)证明:当![]() 且
且![]() 时,总有
时,总有![]()
参考答案:
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)先求函数![]() 导数,根据导函数零点确定函数单调性:先增后减再增,结合图像可知零点个数按两极值正负分情况进行讨论,(2)先研究差函数
导数,根据导函数零点确定函数单调性:先增后减再增,结合图像可知零点个数按两极值正负分情况进行讨论,(2)先研究差函数![]() ,根据导数可得
,根据导数可得![]() ,导函数的导数
,导函数的导数![]() ,因此
,因此![]() ,从而
,从而![]() ,得证.
,得证.
试题解析:解:(Ⅰ) ![]() 零点个数即为方程
零点个数即为方程![]() 的根的个数.
的根的个数.
记![]() ,则
,则![]() ,令
,令![]() 得
得![]() 或
或![]() .
.
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
故可画出![]() 的草图如图所示:
的草图如图所示:

由图象知:当![]() 或
或![]() 时,函数
时,函数![]() 有一个零点;
有一个零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
当![]() 时,函数
时,函数![]() 有三个零点.
有三个零点.
(Ⅱ)![]() ,设函数
,设函数![]() ,
,
则![]() ,
,
记![]() ,则
,则![]() ,
,
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
由上表可知![]() ,而
,而![]() ,
,
由![]() 知,
知, ![]() .
.
所以![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() 在区间
在区间![]() 上为增函数,
上为增函数,
所以当![]() 时,
时, ![]() .
.
即当![]() 且
且![]() 时,
时, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前n项和为Sn , 公差d≠0,且S3+S5=50,a1 , a4 , a13成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 +
+  +…+
+…+  =an﹣1(n∈N*),求数列{nbn}的前n项和Tn .
=an﹣1(n∈N*),求数列{nbn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ,1)上是减函数,求a的取值范围.
,1)上是减函数,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足(an+1﹣1)(an﹣1)=
 (an﹣an+1),a1=2,若bn=
(an﹣an+1),a1=2,若bn=  .
.
(1)证明:数列{bn}是等差数列;
(2)令cn= ,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥
,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥  (n∈N*).
(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
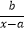 的图象过点A(0,
的图象过点A(0,  ),B(3,3)
),B(3,3)
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(2,+∞)上的单调性,并用单调性的定义加以证明;
(3)若m,n∈(2,+∞)且函数f(x)在[m,n]上的值域为[1,3],求m+n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
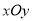 中,点
中,点 ,圆
,圆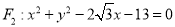 ,以动点
,以动点 为圆心的圆经过点
为圆心的圆经过点 ,且圆
,且圆 与圆
与圆 内切.
内切.(Ⅰ)求动点
 的轨迹
的轨迹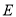 的方程;
的方程;(Ⅱ)若直线
 过点
过点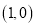 ,且与曲线
,且与曲线 交于
交于 两点,则在
两点,则在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 轴平分
轴平分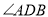 ?若存在,求出
?若存在,求出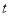 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

