【题目】已知定义域为![]() 的函数
的函数![]() 存在两个零点.
存在两个零点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)分离参数得![]() ,借助函数
,借助函数![]() 的图象进行求解;(2)由于
的图象进行求解;(2)由于![]() ,则
,则![]() 在区间
在区间![]() 上单调递增,
上单调递增, ![]()
![]()
 ,故只需证明
,故只需证明 即可。由题知
即可。由题知![]() 且
且![]() ,不妨设
,不妨设![]() ,则
,则![]() ,构造
,构造![]() ,只需证明
,只需证明![]() 即可,利用导数的知识可求解。
即可,利用导数的知识可求解。
试题解析:
(1)由![]() .得
.得![]() 。
。
令![]() ,则
,则![]() ,
,
当![]() 变化时,
变化时, ![]() 及
及![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| - | 0 | + |
| 减 | 最小 | 增 |
由表可知,当![]() 时,
时, ![]() 有极小值,也为最小值,且最小值为
有极小值,也为最小值,且最小值为![]() ,
,
当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,
,
∴ ![]()
故![]() 在区间
在区间![]() 上存在两个零点时,
上存在两个零点时, ![]() 的取值范围为
的取值范围为![]() .
.
(2)∵![]() , ∴
, ∴ ![]() ,
,
又![]() ,
,
∴![]()
 ,
,
令![]() ,
,
则 ,
,
由题知![]() 且
且![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
∴![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 单调递减,
单调递减,
∴![]() 时,
时, ![]() ,
,
∴ ,
,
又![]() ,
,
∴  ,即
,即![]() ,
,
∴![]() ,
,
∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() ,得证.
,得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
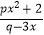 是奇函数,且f(2)=﹣
是奇函数,且f(2)=﹣ 
(1)求函数f(x)的解析式
(2)判断函数f(x)在(0,1)上的单调性,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)设f(x)=
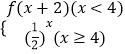 ,求f(1+log23)的值;
,求f(1+log23)的值;
(Ⅱ)已知g(x)=ln[(m2﹣1)x2﹣(1﹣m)x+1]的定义域为R,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司研发出一款新产品,批量生产前先同时在甲、乙两城市销售30天进行市场调查.调查结果发现:甲城市的日销售量
 与天数
与天数 的对应关系服从图①所示的函数关系;乙城市的日销售量
的对应关系服从图①所示的函数关系;乙城市的日销售量 与天数
与天数 的对应关系服从图②所示的函数关系;每件产品的销售利润
的对应关系服从图②所示的函数关系;每件产品的销售利润 与天数
与天数 的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
的对应关系服从图③所示的函数关系,图①是抛物线的一部分.图①
 ,图②
,图② ,图③
,图③
(1)设该产品的销售时间为
 ,日销售利润为
,日销售利润为 ,求
,求 的解析式;
的解析式;(2)若在30天的销售中,日销售利润至少有一天超过2万元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为函数f(x)的不动点.已知f(x)=x2+bx+c
(1)若f(x)有两个不动点为﹣3,2,求函数y=f(x)的零点?
(2)若c= 时,函数f(x)没有不动点,求实数b的取值范围?
时,函数f(x)没有不动点,求实数b的取值范围? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=
 ,动点D在线段AB上.
,动点D在线段AB上.
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
相关试题

