【题目】(Ⅰ)设f(x)= 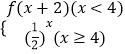 ,求f(1+log23)的值;
,求f(1+log23)的值;
(Ⅱ)已知g(x)=ln[(m2﹣1)x2﹣(1﹣m)x+1]的定义域为R,求实数m的取值范围.
参考答案:
【答案】解:(Ⅰ)∵1+log23∈(2,3),
∴ ![]() ;
;
(Ⅱ)由题设得:(m2﹣1)x2﹣(1﹣m)x+1>0(*)在x∈R时恒成立,
若m2﹣1=0m=±1,
当m=1时,(*)式可化为:1>0恒成立,
当m=﹣1时,(*)式可化为:﹣2x+1>0不恒成立,
∴m=1;
若m2﹣1≠0,
则 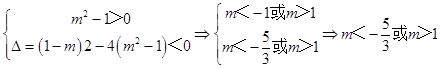
综上,实数m的取值范围是 ![]()
【解析】(I)由1+log23∈(2,3),故f(1+log23)=f(3+log23),进而根据指数的运算性质,可得答案.(II)若g(x)=ln[(m2﹣1)x2﹣(1﹣m)x+1]的定义域为R,则(m2﹣1)x2﹣(1﹣m)x+1>0(*)在x∈R时恒成立,分m2﹣1=0和m2﹣1≠0两种情况结合二次函数的图象和性质,可得满足条件的实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名,现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段






男
3
9
18
15
6
9
女
6
4
5
10
13
2
附表及公式:

0.100
0.050
0.010
0.001
k
2.706
3.841
6.635
10.828

(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上者为优分(含80分),请你根据已知条件作出 列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”. -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
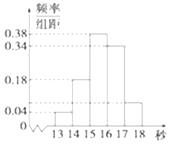
(1)设m,n表示样本中两个学生的百米测试成绩,已知m,n∈[13,14)∪[17,18],求事件“|m-n|>2”的概率;
(2)根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否在犯错误的概率不超过0.01的前提下认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附: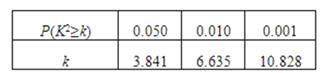
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
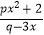 是奇函数,且f(2)=﹣
是奇函数,且f(2)=﹣ 
(1)求函数f(x)的解析式
(2)判断函数f(x)在(0,1)上的单调性,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
 的函数
的函数 存在两个零点.
存在两个零点.(1)求实数
 的取值范围;
的取值范围;(2)若
 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司研发出一款新产品,批量生产前先同时在甲、乙两城市销售30天进行市场调查.调查结果发现:甲城市的日销售量
 与天数
与天数 的对应关系服从图①所示的函数关系;乙城市的日销售量
的对应关系服从图①所示的函数关系;乙城市的日销售量 与天数
与天数 的对应关系服从图②所示的函数关系;每件产品的销售利润
的对应关系服从图②所示的函数关系;每件产品的销售利润 与天数
与天数 的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
的对应关系服从图③所示的函数关系,图①是抛物线的一部分.图①
 ,图②
,图② ,图③
,图③
(1)设该产品的销售时间为
 ,日销售利润为
,日销售利润为 ,求
,求 的解析式;
的解析式;(2)若在30天的销售中,日销售利润至少有一天超过2万元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
相关试题

