【题目】已知椭圆G: ![]() +
+ ![]() =1(b>0)的上、下顶点和右焦点分别为M、N和F,且△MFN的面积为4
=1(b>0)的上、下顶点和右焦点分别为M、N和F,且△MFN的面积为4 ![]() .
.
(1)求椭圆G的方程;
(2)若斜率为1的直线l与椭圆G交于A、B两点.以AB为底作等腰三角形,顶点为P(﹣3,2),求△PAB的面积.
参考答案:
【答案】
(1)
解:∵椭圆G: ![]() +
+ ![]() =1(b>0),c2=3b2﹣b2=2b2,即c=
=1(b>0),c2=3b2﹣b2=2b2,即c= ![]() b,
b,
由△MFN的面积为4 ![]() ,则
,则 ![]() ×2b×c=4
×2b×c=4 ![]() ,即bc=4
,即bc=4 ![]() ,
,
则b=2,a2=3b2=12,
∴椭圆G的方程为: ![]()
(2)
解:设直线l的方程为y=x+m,由  ,整理得4x2+6mx+3m2﹣12=0.①
,整理得4x2+6mx+3m2﹣12=0.①
设A(x1,y1),B(x2,y2)(x1<x2),AB的中点为E(x0,y0),
则x0= ![]() =﹣
=﹣ ![]() ,y0=x0+m=
,y0=x0+m= ![]() ,
,
因为AB是等腰△PAB的底边,则PE⊥AB.
∴PE的斜率k= ![]() =﹣1,解得m=﹣2,
=﹣1,解得m=﹣2,
此时方程①为4x2+12x=0,解得x1=﹣3,x2=0,
∴y1=﹣1,y2=2.
∴|AB|= ![]() =33
=33 ![]() .
.
此时,点P(﹣3,2)到直线AB:x﹣y+2=0的距离d= ![]() =
= ![]() ,
,
∴△PAB的面积S= ![]() |AB|d=
|AB|d= ![]() ,
,
△PAB的面积 ![]()
【解析】(1)由题意方程,求得c= ![]() b,根据三角形的面积公式,求得bc=4
b,根据三角形的面积公式,求得bc=4 ![]() ,即可求得a和b的值,即可求得椭圆方程;(2)设直线方程,代入椭圆方程,利用韦达定理及中点坐标公式,求得m的值,代入求得A和B的坐标,利用两点之间坐标公式及三角形的面积公式,即可求得△PAB的面积.
,即可求得a和b的值,即可求得椭圆方程;(2)设直线方程,代入椭圆方程,利用韦达定理及中点坐标公式,求得m的值,代入求得A和B的坐标,利用两点之间坐标公式及三角形的面积公式,即可求得△PAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,函数y=
 +
+  的定义域为A,函数y=
的定义域为A,函数y=  的定义域为B.
的定义域为B.
(1)求集合A、B.
(2)(UA)∪(UB). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(0,+∞),f(2)=1,f(xy)=f(x)+f(y)且当x>1时,f(x)>0.
(1)判断函数f(x)在其定义域(0,+∞)上的单调性并证明;
(2)解不等式f(x)+f(x﹣2)≤3. -
科目: 来源: 题型:
查看答案和解析>>【题目】设0<a≤
 ,若满足不等式|x﹣a|<b的一切实数x,亦满足不等式|x﹣a2|<
,若满足不等式|x﹣a|<b的一切实数x,亦满足不等式|x﹣a2|<  ,求实数b的取值范围.
,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
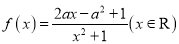 ,其中
,其中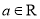 .
.(1)当
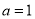 时,求曲线
时,求曲线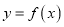 在点
在点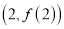 处的切线方程;
处的切线方程;(2)当
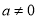 时,求函数
时,求函数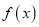 的单调区间与极值.
的单调区间与极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}:
 ,
,  +
+  ,
,  +
+  +
+  ,
, 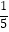 +
+ 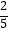 +
+ 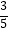 +
+ 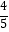 ,…,那么数列{bn}={
,…,那么数列{bn}={  }的前n项和为( )
}的前n项和为( )
A.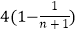
B.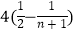
C.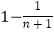
D.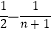
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c和一次函数g(x)=﹣bx,其中a,b,c∈R且满足a>b>c,f(1)=0.
(1)证明:函数f(x)与g(x)的图象交于不同的两点;
(2)若函数F(x)=f(x)﹣g(x)在[2,3]上的最小值为9,最大值为21,试求a,b的值.
相关试题

