【题目】已知二次函数f(x)=ax2+bx+c和一次函数g(x)=﹣bx,其中a,b,c∈R且满足a>b>c,f(1)=0.
(1)证明:函数f(x)与g(x)的图象交于不同的两点;
(2)若函数F(x)=f(x)﹣g(x)在[2,3]上的最小值为9,最大值为21,试求a,b的值.
参考答案:
【答案】
(1)证明:由已知f(1)=0,得:a+b+c=0,
而a>b>c,
∴a>0,c<0,∴ac<0,
∴△=4b2﹣4ac>0;
因此函数f(x)与g(x)图象交于不同的两点;
(2)解:由题意知,F(x)=ax2+2bx+c
∴函数F(x)的图象的对称轴方程为x=﹣ ![]() ,又∵a+b+c=0
,又∵a+b+c=0
∴x= ![]() =1+
=1+ ![]() <1
<1
又a>0
∴F(x)在[2,3]单增
∴ ![]() ,
,
即 ![]() ,
,
∴ ![]()
【解析】(1)由已知中二次函数f(x)=ax2+bx+c和一次函数g(x)=﹣bx,分别求出a>0,c<0,易根据二次方程根的个数及△的关系,得到答案.(2)由题意可得F(x)=ax2+2bx+c,我们可根据二次函数在闭区间上的最值求法,结合函数F(x)在[2,3]上的最小值是9,最大值为21,构造关于a,b的方程,解方程即可求出答案.
【考点精析】本题主要考查了函数的最值及其几何意义和二次函数的性质的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆G:
 +
+  =1(b>0)的上、下顶点和右焦点分别为M、N和F,且△MFN的面积为4
=1(b>0)的上、下顶点和右焦点分别为M、N和F,且△MFN的面积为4 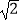 .
.
(1)求椭圆G的方程;
(2)若斜率为1的直线l与椭圆G交于A、B两点.以AB为底作等腰三角形,顶点为P(﹣3,2),求△PAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
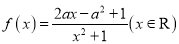 ,其中
,其中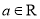 .
.(1)当
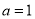 时,求曲线
时,求曲线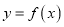 在点
在点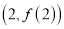 处的切线方程;
处的切线方程;(2)当
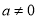 时,求函数
时,求函数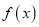 的单调区间与极值.
的单调区间与极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}:
 ,
,  +
+  ,
,  +
+  +
+  ,
, 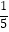 +
+ 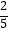 +
+ 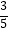 +
+ 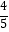 ,…,那么数列{bn}={
,…,那么数列{bn}={  }的前n项和为( )
}的前n项和为( )
A.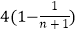
B.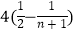
C.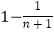
D.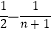
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a=2,解不等式f(x)≥2;
(2)已知f(x)是偶函数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S=
 (b2+c2﹣a2),则∠B=( )
(b2+c2﹣a2),则∠B=( )
A.90°
B.60°
C.45°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的奇函数f(x),当x>0时,f(x)=x﹣2
(1)求函数f(x)的解析式;
(2)求不等式f(x)<2的解集.
相关试题

