【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求函数
时,求函数![]() 的单调区间与极值.
的单调区间与极值.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析: (1)利用导数的几何意义:切线斜率等于![]() ,再根据点斜式求切线方程;(2)先明确函数的定义域,再求函数导数,研究导函数在定义域上的零点: 由
,再根据点斜式求切线方程;(2)先明确函数的定义域,再求函数导数,研究导函数在定义域上的零点: 由![]() ,得
,得![]() ,分类讨论两个零点的大小,再结合列表确定函数的单调区间与极值.
,分类讨论两个零点的大小,再结合列表确定函数的单调区间与极值.
试题解析:(1)当![]() 时,
时, ![]() ,此时
,此时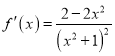 ,
,
所以![]()
又因为切点为![]() ,所以切线方程
,所以切线方程![]()
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(2)由于![]() ,
,
所以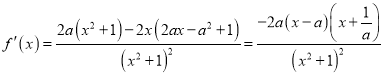
由![]() ,得
,得![]()
(1)当![]() 时,则
时,则![]() ,易得
,易得![]() 在区间
在区间![]() ,
, ![]() 内为减函数,
内为减函数,
在区间![]() 为增函数,故函数
为增函数,故函数![]() 在
在![]() 处取得极小值
处取得极小值![]()
函数![]() 在
在![]() 处取得极大值
处取得极大值![]()
当![]() 时,则
时,则![]() ,易得
,易得![]() 在区间
在区间![]() ,
, ![]() 内为增函数,
内为增函数,
在区间![]() 为减函数,故函数
为减函数,故函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ;
;
函数 ![]() 在
在![]() 处取得极大值
处取得极大值![]()
点睛:本题考查导数的几何意义,属于基础题目. 函数y=f(x)在x=x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,y0)处的切线的斜率![]() ,过点P的切线方程为:
,过点P的切线方程为: ![]() .求函数y=f(x)在点P(x0,y0)处的切线方程与求函数y=f(x)过点P(x0,y0)的切线方程意义不同,前者切线有且只有一条,且方程为y-y0=f′(x0)(x-x0),后者可能不只一条.
.求函数y=f(x)在点P(x0,y0)处的切线方程与求函数y=f(x)过点P(x0,y0)的切线方程意义不同,前者切线有且只有一条,且方程为y-y0=f′(x0)(x-x0),后者可能不只一条.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
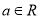 ,函数
,函数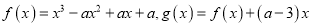 .
.(1)求证:曲线
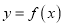 在点
在点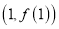 处的切线过定点;
处的切线过定点;(2)若
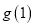 是
是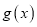 在区间
在区间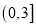 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数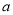 的取值范围;
的取值范围;(3)求证:对任意给定的正数
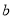 ,总存在
,总存在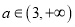 ,使得
,使得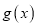 在
在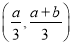 上为单调函数.
上为单调函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
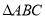 的三个顶点分别为是
的三个顶点分别为是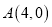 ,
,  ,
, 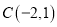 .
.(Ⅰ)求
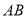 边上的高
边上的高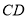 所在的直线方程;
所在的直线方程;(Ⅱ)求过点
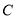 且在两坐标轴上的截距相等的直线方程.
且在两坐标轴上的截距相等的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
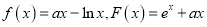 ,其中
,其中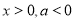 .
.(1)若
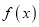 和
和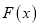 在区间
在区间 上具有相同的单调性,求实数
上具有相同的单调性,求实数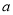 的取值范围;
的取值范围;(2)若
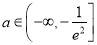 ,且函数
,且函数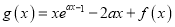 的最小值为
的最小值为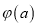 ,求
,求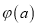 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
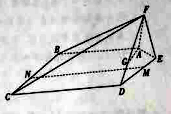
如图,在五棱锥
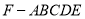 中,
中,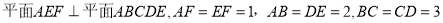 ,且
,且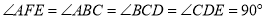 .
.
(1)已知点
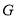 在线段
在线段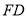 上,确定
上,确定 的位置,使得
的位置,使得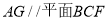 ;
;(2)点
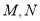 分别在线段
分别在线段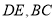 上,若沿直线
上,若沿直线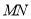 将四边形
将四边形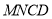 向上翻折,
向上翻折, 与
与 恰好重合,求直线
恰好重合,求直线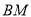 与平面
与平面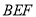 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在透明塑料制成的长方体
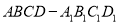 容器内灌进一些水(未满),现将容器底面一边
容器内灌进一些水(未满),现将容器底面一边 固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:①水的部分始终呈棱柱状;
②水面四边形
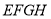 的面积为定值;
的面积为定值;③棱
 始终与水面
始终与水面 平行;
平行;④若
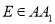 ,
,  ,则
,则 是定值.
是定值.则其中正确命题的个数的是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若对于定义在
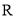 上的连续函数
上的连续函数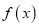 ,存在常数
,存在常数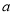 (
(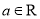 ),使得
),使得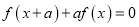 对任意的实数
对任意的实数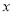 成立,则称
成立,则称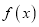 是回旋函数,且阶数为
是回旋函数,且阶数为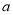 .
.(1)试判断函数
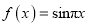 是否是一个阶数为1的回旋函数,并说明理由;
是否是一个阶数为1的回旋函数,并说明理由;(2)已知
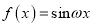 是回旋函数,求实数
是回旋函数,求实数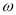 的值;
的值;(3)若回旋函数
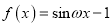 (
(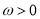 )在
)在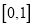 恰有100个零点,求实数
恰有100个零点,求实数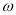 的值.
的值.
相关试题

