【题目】如图,在平面直角坐标系中,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .
.
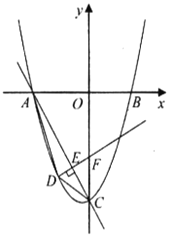
(1)求抛物线的解析式;
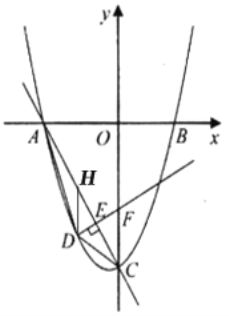
(2)如图,点![]() 是直线
是直线![]() 下方抛物线上的一个动点,连结
下方抛物线上的一个动点,连结![]() .当
.当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)如图,在(2)的条件下,过点![]() 作于
作于![]() 点
点![]() 交
交![]() 轴于点
轴于点![]() 将
将![]() 绕点
绕点![]() 旋转得到
旋转得到![]() 在旋转过程中,当点
在旋转过程中,当点![]() 或点
或点![]() 落在
落在![]() 轴上(不与点
轴上(不与点![]()
![]() 重合)时,将
重合)时,将![]() 沿射线
沿射线![]() 平移得到
平移得到![]() ,在平移过程中,平面内是否存在点
,在平移过程中,平面内是否存在点![]() 使得四边形
使得四边形![]() 是菱形?若存在,请直接写出所有符合条件的点
是菱形?若存在,请直接写出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3) 所有符合条件的点
;(3) 所有符合条件的点![]() 坐标为
坐标为![]() 或
或![]()
【解析】
(1)分别根据对称轴方程,再代入点的坐标进行求解即可.
(2) 过![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,进而根据
,进而根据![]() 表达出
表达出![]() 关于
关于![]() 的横坐标的表达式,再根据二次函数的最值求解即可.
的横坐标的表达式,再根据二次函数的最值求解即可.
(3)分两种情况,设平移的距离为![]() ,再根据菱形满足
,再根据菱形满足![]() 即可求得
即可求得![]() ,进而根据菱形的性质可求得
,进而根据菱形的性质可求得![]()
![]() 抛物线对称轴为
抛物线对称轴为![]() .
.
且点![]() 的坐标为
的坐标为![]() .点
.点![]() 的坐标为
的坐标为![]()
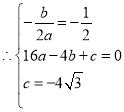 .解得
.解得
![]() 抛物线的解析式为
抛物线的解析式为![]()
(2)过![]() 作
作![]() 轴交
轴交![]() 于
于![]() .设
.设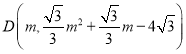 ,
,
设![]() 的解析式为
的解析式为![]() ,则
,则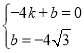 ,解得
,解得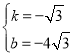 .
.
故![]() 的解析式为
的解析式为![]() .则
.则![]()
则![]()
![]() .
.
故当![]() 时,
时,![]() 取最大值
取最大值![]() .此时
.此时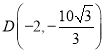
(3) 存在,所有符合条件的![]() 坐标为
坐标为![]() ,
,![]() .
.
提示: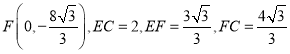 .
.
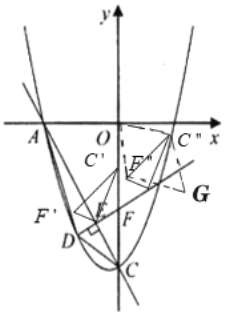
①当![]() 落在
落在![]() 轴上时,如图,点
轴上时,如图,点![]() ,
,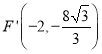 ,
,
设平移距离是![]() ,则
,则![]() ,
,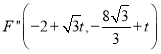 .
.
由![]() 得
得 ,解得
,解得![]() .
.
此时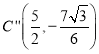 ,
,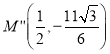 ,所以
,所以![]() .
.
②当![]() 落在
落在![]() 轴上时,如图,点
轴上时,如图,点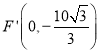 ,
,![]() ,
,
设平移距离是![]() ,则
,则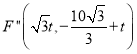 ,
,![]() .
.
由![]() 得
得 ,解得
,解得![]() .
.
此时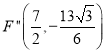 ,
,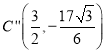 ,所以
,所以![]() .
.
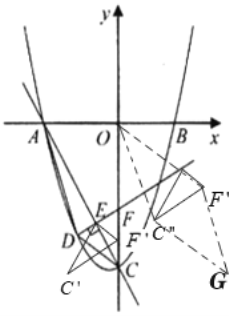
综上所述,所有符合条件的点![]() 坐标为
坐标为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】全国校足办决定于2019年8月组织开展全国青少年校园足球夏令营总营活动.某校购买
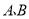 两种不同品牌的足球,其中
两种不同品牌的足球,其中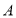 种品牌足球
种品牌足球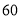 个,
个,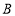 种品牌足球
种品牌足球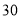 个,共需元
个,共需元 ,已知
,已知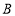 种品牌足球的售价比
种品牌足球的售价比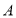 种品牌足球的售价高
种品牌足球的售价高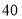 元/个.
元/个.(1)求
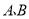 两种品牌足球的售价;
两种品牌足球的售价;(2)该校为举办足球联谊赛,决定第二次购买
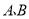 两种不同品牌的足球.恰逄商场对两种品牌足球的售价进行调整,
两种不同品牌的足球.恰逄商场对两种品牌足球的售价进行调整,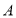 种品牌足球售价比第一次购买时提高了
种品牌足球售价比第一次购买时提高了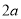 元/个
元/个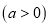 ,
,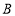 种品牌足球按第一次购买时售价的
种品牌足球按第一次购买时售价的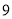 折(即原价的
折(即原价的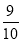 )出售.如果第二次购买
)出售.如果第二次购买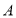 种品牌足球的个数比第一次少
种品牌足球的个数比第一次少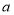 个,第二次购买
个,第二次购买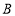 种品牌足球的个数比第一次多
种品牌足球的个数比第一次多 个,则第二次购买
个,则第二次购买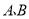 两种品牌足球的总费用比第一次少
两种品牌足球的总费用比第一次少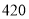 元.求
元.求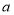 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
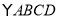 中,
中,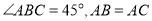 ,点
,点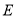 在边
在边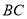 上,连结
上,连结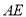 .
.
(1)若
 ,求
,求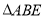 的周长;
的周长;(2)点
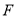 是
是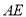 上一点,连结
上一点,连结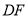 交
交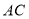 于点
于点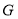 .
.①如图2,若
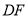 平分
平分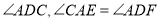 ,求证:
,求证: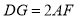 ;
;②如图3,连结
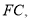 过点
过点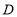 作
作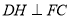 交
交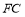 的延长线于点
的延长线于点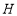 ,且
,且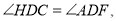 延长
延长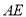 交
交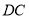 延长线于点
延长线于点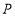 ,请直接写出线段
,请直接写出线段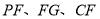 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为3的正
 的各边三等分,过每个分点分别作另外两边的平行线,称
的各边三等分,过每个分点分别作另外两边的平行线,称 的边及这些平行线所交的10个点为格点.若在这10个格点中任取
的边及这些平行线所交的10个点为格点.若在这10个格点中任取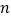 个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求
个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求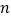 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据中的每一个数据都乘以2,再减去80,得到一组新数据,若求得新的数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.40.6,1.1B.48.8,4.4C.81.2,44.4D.78.8,75.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为 ,满足
,满足 .
.(1) 求角
 的大小;
的大小;(2) 若
 ,求
,求 ,
, 的值.(其中
的值.(其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】 2013年春节前,有超过20万名来自广西、四川的外来务工人员选择驾乘摩托车沿321国道返乡过年,为防止摩托车驾驶人员因长途疲劳驾驶而引发交通事故,肇庆市公安交警部门在321国道沿线设立了多个休息站,让过往的摩托车驾驶人员有一个停车休息的场所.交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就对其省籍询问一次,询问结果如图所示:

(1)交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?
相关试题

