【题目】在![]() 中,三个内角
中,三个内角![]() 所对的边分别为
所对的边分别为![]() ,满足
,满足![]() .
.
(1) 求角![]() 的大小;
的大小;
(2) 若![]() ,求
,求![]() ,
,![]() 的值.(其中
的值.(其中![]() )
)
参考答案:
【答案】(1)![]() ;(2)4,6
;(2)4,6
【解析】
(1)已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式化简,求出![]() 的值,即可确定出
的值,即可确定出![]() 的度数;(2)根据平面向量数量积的运算法则计算得到一个等式
的度数;(2)根据平面向量数量积的运算法则计算得到一个等式![]() ,记作①,把
,记作①,把![]() 的度数代入求出
的度数代入求出![]() 的值,记作②,然后利用余弦定理表示出
的值,记作②,然后利用余弦定理表示出![]() ,把
,把![]() 及
及![]() 的值代入求出
的值代入求出![]() 的值,利用完全平方公式表示出
的值,利用完全平方公式表示出![]() ,把相应的值代入,开方求出
,把相应的值代入,开方求出![]() 的值,由②③可知
的值,由②③可知![]() 与
与![]() 为一个一元二次方程的两个解,求出方程的解,根据
为一个一元二次方程的两个解,求出方程的解,根据![]() 大于
大于![]() ,可得出
,可得出![]() ,
,![]() 的值.
的值.
(1)已知等式![]() ,
,
利用正弦定理化简得![]() ,
,
整理得![]() ,
,
即![]() ,
,
![]() ,
,
则![]() .
.
(2)由![]() ,得
,得![]() , ①
, ①
又由(1)![]() ,②
,②
由余弦定理得![]() ,
,
将![]() 及①代入得
及①代入得![]() ,
,
![]() ,
,
![]() ,③
,③
由②③可知![]() 与
与![]() 为一个一元二次方程
为一个一元二次方程![]() 的两个根,
的两个根,
解此方程,并由![]() 大于
大于![]() ,可得
,可得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
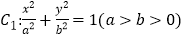 和双曲线
和双曲线 有共同的焦点
有共同的焦点 ,
,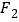 ,点
,点 是
是 ,
, 的交点,若
的交点,若 是锐角三角形,则椭圆
是锐角三角形,则椭圆 离心率
离心率 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度
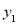 与时间t满足关系式:
与时间t满足关系式: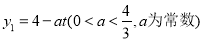 ,若使用口服方式给药,则药物在白鼠血液内的浓度
,若使用口服方式给药,则药物在白鼠血液内的浓度 与时间t满足关系式:
与时间t满足关系式: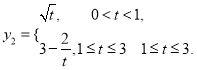 现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中,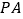 ⊥底面
⊥底面 ,
, 是
是 的中点.
的中点.已知
 ,
, ,
, ,
, .求:
.求:(1)三棱锥PABC的体积;
(2)异面直线BC与AD所成角的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动.为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个小组中随机抽取10名学生参加问卷调查.各组人数统计如下:

(1)从参加问卷调查的10名学生中随机抽取两名,求这两名学生来自同一个小组的概率;
(2)在参加问卷调查的10名学生中,从来自甲、丙两个小组的学生中随机抽取两名,用
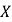 表示抽得甲组学生的人数,求
表示抽得甲组学生的人数,求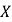 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为1正方体
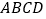 中,点
中,点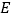 ,
,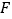 分别为边
分别为边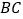 ,
,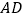 的中点,将
的中点,将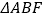 沿
沿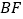 所在的直线进行翻折,将
所在的直线进行翻折,将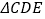 沿
沿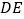 所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
所在直线进行翻折,在翻折的过程中,下列说法错误的是( )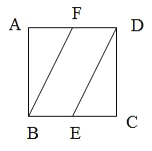
A. 无论旋转到什么位置,
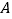 、
、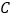 两点都不可能重合
两点都不可能重合B. 存在某个位置,使得直线
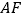 与直线
与直线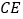 所成的角为
所成的角为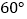
C. 存在某个位置,使得直线
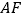 与直线
与直线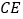 所成的角为
所成的角为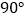
D. 存在某个位置,使得直线
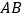 与直线
与直线 所成的角为
所成的角为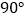
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点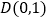 ,且离心率为
,且离心率为 .过抛物线
.过抛物线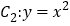 上一点
上一点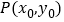 作
作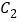 的切线
的切线 交椭圆
交椭圆 于
于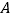 ,
,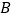 两点.
两点.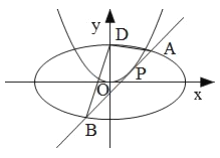
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)是否存在直线
 ,使得
,使得 ,若存在,求出
,若存在,求出 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
相关试题

