【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值

参考答案:
【答案】(I)见解析;(II)![]() .
.
【解析】试题本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力。满分15分。
(Ⅰ)取PA中点F,构造平行四边形BCEF,可证明;(Ⅱ)由题意,取BC,AD的中点M,N,可得AD⊥平面PBN,即BC⊥平面PBN,过点Q作PB的垂线,垂足为H,连结MH.可知MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.依此可在Rt△MQH中,求∠QMH的正弦值.
试题解析:
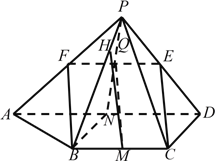
(Ⅰ)如图,设PA中点为F,连接EF,FB.
因为E,F分别为PD,PA中点,所以![]() 且
且![]() ,
,
又因为![]() ,
, ![]() ,所以
,所以![]() 且
且![]() ,
,
即四边形BCEF为平行四边形,所以![]() ,
,
因此![]() 平面PAB.
平面PAB.
(Ⅱ)分别取BC,AD的中点为M,N.连接PN交EF于点Q,连接MQ.
因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,
在平行四边形BCEF中,MQ//CE.
由△PAD为等腰直角三角形得PN⊥AD.
由DC⊥AD,N是AD的中点得BN⊥AD.
所以AD⊥平面PBN,
由BC//AD得BC⊥平面PBN,
那么平面PBC⊥平面PBN.
过点Q作PB的垂线,垂足为H,连接MH.
MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.
设CD=1.
在△PCD中,由PC=2,CD=1,PD=![]() 得CE=
得CE=![]() ,
,
在△PBN中,由PN=BN=1,PB=![]() 得QH=
得QH=![]() ,
,
在Rt△MQH中,QH=![]() ,MQ=
,MQ=![]() ,
,
所以sin∠QMH=![]() ,
,
所以直线CE与平面PBC所成角的正弦值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,侧棱
中,侧棱 底面
底面 ,
,  为棱
为棱 中点.
中点. 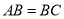 ,
,  ,
,  .
.
(I)求证:
 平面
平面 .
.(II)求证:
 平面
平面 .
.(III)在棱
 的上是否存在点
的上是否存在点 ,使得平面
,使得平面 平面
平面 ?如果存在,求此时
?如果存在,求此时 的值;如果不存在,说明理由.
的值;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解关于x的不等式

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学要从高一年级甲、乙两个班级中选择一个班参加市电视台组织的“环保知识竞赛”.该校对甲、乙两班的参赛选手(每班7人)进行了一次环境知识测试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85分,乙班学生成绩的中位数是85.

(1)求
 的值;
的值;(2)根据茎叶图,求甲、乙两班同学成绩的方差的大小,并从统计学角度分析,该校应选择甲班还是乙班参赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是
是 在点
在点 处的切线.
处的切线.(
 )求
)求 的解析式.
的解析式.(
 )求证:
)求证:  .
.(
 )设
)设 ,其中
,其中 .若
.若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列函数的最值
(1)求函数
 的最小值.
的最小值.(2)求函数
 的最小值.
的最小值.(3)设
 ,
, ,若
,若 ,求
,求 的最小值.
的最小值.(4)若正数
 ,
, 满足
满足 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集
 ,其中
,其中 ,
,  ,定义向量集
,定义向量集 .若对于任意
.若对于任意 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .例如
.例如 具有性质
具有性质 .
.(
 )若
)若 ,且
,且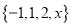 具有性质
具有性质 ,求
,求 的值.
的值.(
 )若
)若 具有性质
具有性质 ,求证:
,求证:  ,且当
,且当 时,
时,  .
.(
 )若
)若 具有性质
具有性质 ,且
,且 ,
,  (
( 为常数),求有穷数列
为常数),求有穷数列 ,
,  ,
,  ,
,  的通项公式.
的通项公式.
相关试题

