【题目】设![]() 是
是![]() 在点
在点![]() 处的切线.
处的切线.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )求证:
)求证: ![]() .
.
(![]() )设
)设![]() ,其中
,其中![]() .若
.若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】试题分析:(1)第(1)问,利用导数的几何意义求切线方程即得y=f(x). (2)第(2)问,转化成证明![]() ,即证明[f(x)-g(x)]的最大值小于等于零.(3),第(3)问,对a分类讨论,求函数
,即证明[f(x)-g(x)]的最大值小于等于零.(3),第(3)问,对a分类讨论,求函数![]() 的单调区间和最小值,找到a的范围.
的单调区间和最小值,找到a的范围.
试题解析:
(![]() )由
)由![]() 得
得![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,即
,即![]() ,
,
∴![]() 的解析式为:
的解析式为: ![]() .
.
(![]() )令
)令![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
(![]() )
)![]() 的定义域是
的定义域是![]() ,且
,且![]() .
.
①![]() 时,由(
时,由(![]() )得:
)得: ![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 恒成立,符合题意;
恒成立,符合题意;
②![]() 时,由
时,由![]() ,且
,且![]() 的导数
的导数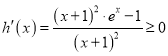 ,
,
∴![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∵![]() ,
, ![]() ,
,
∴存在![]() ,使得
,使得![]() ,
,
∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,∴
上单调递增,∴![]() ,
,
此时, ![]() 不可能恒成立,不符合题意,
不可能恒成立,不符合题意,
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解关于x的不等式

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学要从高一年级甲、乙两个班级中选择一个班参加市电视台组织的“环保知识竞赛”.该校对甲、乙两班的参赛选手(每班7人)进行了一次环境知识测试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85分,乙班学生成绩的中位数是85.

(1)求
 的值;
的值;(2)根据茎叶图,求甲、乙两班同学成绩的方差的大小,并从统计学角度分析,该校应选择甲班还是乙班参赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值

-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列函数的最值
(1)求函数
 的最小值.
的最小值.(2)求函数
 的最小值.
的最小值.(3)设
 ,
, ,若
,若 ,求
,求 的最小值.
的最小值.(4)若正数
 ,
, 满足
满足 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集
 ,其中
,其中 ,
,  ,定义向量集
,定义向量集 .若对于任意
.若对于任意 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .例如
.例如 具有性质
具有性质 .
.(
 )若
)若 ,且
,且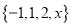 具有性质
具有性质 ,求
,求 的值.
的值.(
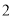 )若
)若 具有性质
具有性质 ,求证:
,求证:  ,且当
,且当 时,
时,  .
.(
 )若
)若 具有性质
具有性质 ,且
,且 ,
,  (
( 为常数),求有穷数列
为常数),求有穷数列 ,
,  ,
,  ,
,  的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,平面多边形
 中,AE=ED,AB=BD,且
中,AE=ED,AB=BD,且 ,现沿直线
,现沿直线 ,将
,将 折起,得到四棱锥
折起,得到四棱锥 .
.
(1)求证:
 ;
;(2)若
 ,求PD与平面
,求PD与平面 所成角的正弦值.
所成角的正弦值.
相关试题

