【题目】解关于x的不等式![]()
参考答案:
【答案】见解析
【解析】
根据a的范围,分a等于0和a大于0两种情况考虑:当![]() 时,把
时,把![]() 代入不等式得到一个一元一次不等式,求出不等式的解集;当a大于0时,把原不等式的左边分解因式,再根据a大于1,
代入不等式得到一个一元一次不等式,求出不等式的解集;当a大于0时,把原不等式的左边分解因式,再根据a大于1,![]() 及a大于0小于1分三种情况取解集,当a大于1时,根据
及a大于0小于1分三种情况取解集,当a大于1时,根据![]() 小于1,利用不等式取解集的方法求出解集;当
小于1,利用不等式取解集的方法求出解集;当![]() 时,根据完全平方式大于0,得到x不等于1;当a大于0小于1时,根据
时,根据完全平方式大于0,得到x不等于1;当a大于0小于1时,根据![]() 大于1,利用不等式取解集的方法即可求出解集,综上,写出a不同取值时,各自的解集即可.
大于1,利用不等式取解集的方法即可求出解集,综上,写出a不同取值时,各自的解集即可.
当![]() 时,不等式化为
时,不等式化为![]() ,
,![]() ;
;
当![]() 时,原不等式化为
时,原不等式化为![]() ,
,
![]() 当
当![]() 时,不等式的解为
时,不等式的解为![]() 或
或![]() ;
;
![]() 当
当![]() 时,不等式的解为
时,不等式的解为![]() ;
;
![]() 当
当![]() 时,不等式的解为
时,不等式的解为![]() 或
或![]() ;
;
综上所述,得原不等式的解集为:
当![]() 时,解集为
时,解集为![]() ;当
;当![]() 时,解集为
时,解集为![]() 或
或![]() ;
;
当![]() 时,解集为
时,解集为![]() ;当
;当![]() 时,解集为
时,解集为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,其中实数
,其中实数 满足
满足 ,若
,若 的最大值为
的最大值为 ,则
,则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆的中心在原点,焦点在
 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点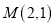 ,平行于
,平行于 的直线
的直线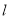 在
在 轴上的截距为
轴上的截距为 ,直线
,直线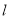 交椭圆于
交椭圆于 两个不同点.
两个不同点.
(1)求椭圆的方程;
(2)求
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
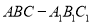 中,侧棱
中,侧棱 底面
底面 ,
,  为棱
为棱 中点.
中点. 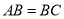 ,
,  ,
,  .
.
(I)求证:
 平面
平面 .
.(II)求证:
 平面
平面 .
.(III)在棱
 的上是否存在点
的上是否存在点 ,使得平面
,使得平面 平面
平面 ?如果存在,求此时
?如果存在,求此时 的值;如果不存在,说明理由.
的值;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学要从高一年级甲、乙两个班级中选择一个班参加市电视台组织的“环保知识竞赛”.该校对甲、乙两班的参赛选手(每班7人)进行了一次环境知识测试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85分,乙班学生成绩的中位数是85.

(1)求
 的值;
的值;(2)根据茎叶图,求甲、乙两班同学成绩的方差的大小,并从统计学角度分析,该校应选择甲班还是乙班参赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是
是 在点
在点 处的切线.
处的切线.(
 )求
)求 的解析式.
的解析式.(
 )求证:
)求证:  .
.(
 )设
)设 ,其中
,其中 .若
.若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

