【题目】已知定点M(﹣ ![]() ),N是圆C:(x﹣
),N是圆C:(x﹣ ![]() )2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
)2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
(1)求动点E的轨迹方程C1;
(2)直线l与轨迹C1交于P,Q两点,与抛物线C2:x2=4y交于A,B两点,且抛物线C2在点A,B处的切线垂直相交于S,设点S到直线l的距离为d,试问:是否存在直线l,使得d= ![]() ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由.
参考答案:
【答案】
(1)解:依题意有:|EM|+|EC|=|EN|+|EC|=|NC|=4,故动点E的轨迹为以M,C为焦点,长轴为4的椭圆.
于是: ![]() ,从而
,从而 ![]() ,故动点E的轨迹方程C1为:
,故动点E的轨迹方程C1为: ![]()
(2)解:设直线l:y=kx+m,A(x1,y1),B(x2,y2),P(x3,y3)Q(x4,y4),由 ![]() ,
,
得:x2﹣4kx﹣4m=0,故x1+x2=4k,x1x2=﹣4m.
由x2=4y得: ![]() ,即切线斜率
,即切线斜率 ![]() .
.
于是: ![]() ,
,
由PA⊥PB得; ![]() ,
,
解得:m=1,
这说明直线l过抛物线C2的焦点F,由 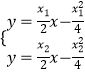 ,
,
得: ![]() 即S(2k,﹣1).
即S(2k,﹣1).
于是:点S(2k,﹣1)到直线l:kx﹣y+1=0的距离 ![]() ,
,
由 ![]() 得:(1+2k2)x2+4kx﹣2=0,
得:(1+2k2)x2+4kx﹣2=0,
从而 ![]() ,
,
同理:|AB|=4(1+k2),
由 ![]() 得
得 ![]() ,
,
化简整理,得:28k4+36k2+7=0,此方程无解,
所以不存在直线l,使得 ![]()
【解析】(1)由题意可知::|EM|+|EC|=|EN|+|EC|=|NC|=4,故动点E的轨迹为以M,C为焦点,长轴为4的椭圆,分别求得a、b和c的值,求得动点E的轨迹方程C1;(2)设出直线l的方程,代入椭圆方程,由韦达定理求得x1+x2及x1x2 , 利用导数法求得直线PA和PB的斜率,由PA⊥PB,求得m的值,直线l过抛物线C2的焦点F,求得交点S的坐标,根据点到直线的距离公式,求得S到到直线l:kx﹣y+1=0的距离d,根据弦长公式求得丨PQ丨及|AB|,由 ![]() ,求得28k4+36k2+7=0,此方程无解,不存在直线l,使得
,求得28k4+36k2+7=0,此方程无解,不存在直线l,使得 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
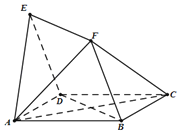
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若变量x,y满足约束条件
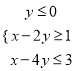 ,则z=3x+5y的取值范围是( )
,则z=3x+5y的取值范围是( )A. [3,+∞) B. [﹣8,3] C. (﹣∞,9] D. [﹣8,9]
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
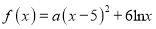 ,其中
,其中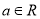 ,曲线
,曲线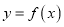 在点
在点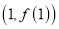 处的切线与
处的切线与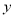 轴相交于点
轴相交于点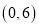 .
.(1)确定
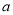 的值;
的值;(2)求函数
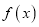 的单调区间与极值.
的单调区间与极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2016年“双十”天猫总成交金额突破1207亿元.某购物网站为优化营销策略,对11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者(其中有女性800名,男性200名)进行抽样分析.采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析,得到下表:(消费金额单位:元)
女性消费情况:
消费金额
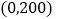
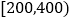
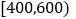
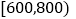
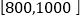
人数
5
10
15
47
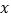
男性消费情况:
消费金额
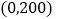
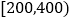
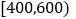
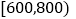
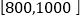
人数
2
3
10
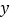
2
(1)计算
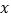 ,
,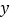 的值;在抽出的100名且消费金额在
的值;在抽出的100名且消费金额在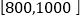 (单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写
 列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”女性
男性
总计
网购达人
非网购达人
总计
附:
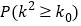
0.10
0.05
0.025
0.010
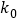
2.706
3.841
5.024
6.635
(
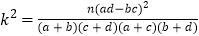 ,其中
,其中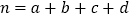 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
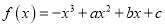 在点
在点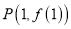 处的切线方程为
处的切线方程为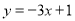 .
.(1)若函数
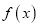 在
在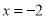 时有极值,求
时有极值,求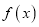 的解析式;
的解析式;(2)函数
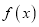 在区间
在区间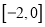 上单调递增,求实数
上单调递增,求实数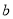 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=ex(ax﹣1),g(x)=a(x﹣1),a∈R.
(1)讨论f(x)的单调性;
(2)若有且仅有两个整数xi(i=1,2),使得f(xi)<g(xi)成立,求实数a的取值范围.
相关试题

