【题目】设![]() ,其中
,其中![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴相交于点
轴相交于点![]() .
.
(1)确定![]() 的值;
的值;
(2)求函数![]() 的单调区间与极值.
的单调区间与极值.
参考答案:
【答案】(1)a=![]() (2)极小值2+6ln 3. 极大值f(2)=
(2)极小值2+6ln 3. 极大值f(2)=![]() +6ln 2,f(x)在(0,2),(3,+∞)上为增函数;
+6ln 2,f(x)在(0,2),(3,+∞)上为增函数;
当2<x<3时,f′(x)<0,故f(x)在(2,3)上为减函数.
【解析】试题分析:(1)求出导数![]() ,得
,得![]() ,写出题中切线方程
,写出题中切线方程![]() ,令
,令![]() ,则
,则![]() ,由此可得
,由此可得![]() ;(2)解不等式
;(2)解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;
得减区间; ![]() 的点就是极值点,由刚才的单调性可知是极大值点还是极小值点.
的点就是极值点,由刚才的单调性可知是极大值点还是极小值点.
试题解析:(1)因为![]() ,
,
故![]() .
.
令![]() ,得
,得![]() ,
, ![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
由点![]() 在切线上,可得
在切线上,可得![]() ,解得
,解得![]() .
.
(2)由(1)知, ![]() (
(![]() ),
),
![]()
![]() .
.
令![]() ,解得
,解得![]() ,
, ![]() .
.
当![]() 或
或![]() 时,
时, ![]() ,故
,故![]() 的递增区间是
的递增区间是![]() ,
, ![]() ;
;
当![]() 时,
时, ![]() ,故
,故![]() 的递减区间是
的递减区间是![]() .
.
由此可知![]() 在
在![]() 处取得极大值
处取得极大值![]() ,
,
在![]() 处取得极小值
处取得极小值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥DC,AE⊥DC,BE∥AD.M、N分别是AD、BE上的点,且AM=BN,将三角形ADE沿AE折起,则下列说法正确的是 (填上所有正确说法的序号).
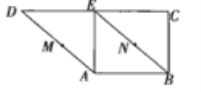
①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;
②不论D折至何位置都有MN⊥AE;
③不论D折至何位置(不在平面ABC内)都有MN∥AB;
④在折起过程中,一定存在某个位置,使EC⊥AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x+1,x∈N*.若x0,n∈N*,使f(x0)+f(x0+1)+…+f(x0+n)=63成立,则称(x0,n)为函数f(x)的一个“生成点”.则函数f(x)的“生成点”共有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,曲线C:(x-1)2+y2=1.直线l经过点P(m,0),且倾斜角为
 ,以O为极点,x轴正半轴为极轴,建立极坐标系.
,以O为极点,x轴正半轴为极轴,建立极坐标系.(1)写出曲线C的极坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据完成下面2×2列联表;
(2)请问能有多大把握认为药物有效?
不得禽流感
得禽流感
总计
服药
不服药
总计
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体ABCD-A1B1C1D1中,E,F分别是AB,AA1的中点.
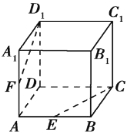
求证:(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.
相关试题

