【题目】已知f(x)=ex(ax﹣1),g(x)=a(x﹣1),a∈R.
(1)讨论f(x)的单调性;
(2)若有且仅有两个整数xi(i=1,2),使得f(xi)<g(xi)成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:因f′(x)=ex(ax+a﹣1).
所以,当a=0时,f′(x)<0在R上恒成立,
即f(x)在(﹣∞,+∞)上单调递减;
当a>0时,f′(x)>0的解为 ![]() ,
,
即f(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减;
上单调递减;
当a<0时,f′(x)>0的解为 ![]() ,
,
即f(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减.
上单调递减.
(2)解:
法一:当a=0时,f(x)=﹣ex,g(x)=0,
此时f(x)<g(x)的解集为R,所以此情况舍去;
当a<0时,f(0)=﹣1<g(0)=﹣a,f(1)=e(a﹣1)<g(1)=0,f(2)=e2(2a﹣1)<g(2)=a.
可见f(x)<g(x)的解集不仅仅两个整数解,此情况舍去;
当a>0时,
由(1)可知f(x)的极值点为 ![]() ,
,
又f(0)=﹣1,g(1)=0, ![]() ,而且,f(x)仅有一个零点
,而且,f(x)仅有一个零点 ![]() .
.
若 ![]() ,即a≥1时,
,即a≥1时,
由(1)知f(x)的单调性,以及 ![]() ,
,
有f(x)与g(x)的草图如下:
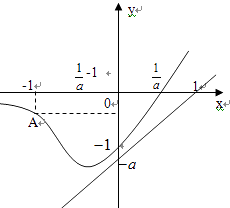
因 ![]() ,
,
所以在(﹣∞,﹣1]上f(x)单调递减,g(x)单调递增,
所以 ![]() .g(x)max=g(﹣1)=﹣2a,
.g(x)max=g(﹣1)=﹣2a,
所以在(﹣∞,﹣1]上f(x)>g(x)恒成立.
又f(0)=﹣1>g(0)=﹣a,在x∈[1,+∞)上,又a≥1,所以,ex>1,ax﹣1≥0,
所以f(x)=ex(ax﹣1)>ax﹣1=a(x﹣1)+a﹣1≥a(x﹣1)=g(x)
所以在a≥1时,在R上没有使得f(x)<g(x)的整数解存在;
若 ![]() ,即o<a<1时,f(x)与g(x)的草图如下:
,即o<a<1时,f(x)与g(x)的草图如下:

因为f(0)=﹣1<﹣a=g(0),f(1)=e(a﹣1)<0=g(1),
若 ![]() ,解得
,解得 ![]() .
.
而由上知在(﹣∞,﹣1)上f(x)>g(x)恒成立,
下证明在x∈[2,+∞)上, ![]() 时,f(x)≥g(x)恒成立,
时,f(x)≥g(x)恒成立,
令函数h(x)=f(x)﹣g(x),x∈[2,+∞),则h'(x)=ex(ax﹣1+a)﹣a,
因为x∈[2,+∞), ![]() ,所以
,所以 ![]() ,
,
所以 ![]() ,
,
即h'(x)>0在x∈[2,+∞)上恒成立,
所以函数h(x)在[2,+∞)上单调递增,所以h(x)≥h(2)=(2e2﹣1)a﹣e2≥0
所以在x∈[2,+∞)上, ![]() 时,f(x)≥g(x)恒成立.
时,f(x)≥g(x)恒成立.
综上: ![]() .
.
法二:若有且仅有两个整数xi(i=1,2),使得f(xi)<g(xi)成立,
则a(xex﹣x+1)<ex有两个整数解.
因为y=x(ex﹣1)+1,当x>0时,ex﹣1>0,x(ex﹣1)+1》>0;
当x<0时,ex﹣1<0,x(ex﹣1)+1》>0,
所以, ![]() 有两个整数解
有两个整数解
设g(x)= ![]() ,则
,则 ![]() ,
,
令h(x)=2﹣x﹣ex,则h′(x)=﹣1﹣ex《<0,
又h(0)=1>0,h((1)=1﹣e<0,
所以x0∈(0,1),使得h(x0)=0,
∴g(x)在为增函数,在(x0,+∞)为减函数,
∴ ![]() 有两个整数解的充要条件是:
有两个整数解的充要条件是:
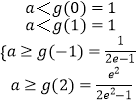 ,
,
解得: ![]()
【解析】(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(2)法一:分别求出f(x)和g(x)的特殊值,通过a的范围,通过观察f(x),g(x)的图象求出a的范围即可;法二:分离参数,问题转化为 ![]() 有两个整数解,得到关于a的不等式组,解出即可.
有两个整数解,得到关于a的不等式组,解出即可.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的最大(小)值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定点M(﹣
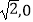 ),N是圆C:(x﹣
),N是圆C:(x﹣ 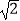 )2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
)2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
(1)求动点E的轨迹方程C1;
(2)直线l与轨迹C1交于P,Q两点,与抛物线C2:x2=4y交于A,B两点,且抛物线C2在点A,B处的切线垂直相交于S,设点S到直线l的距离为d,试问:是否存在直线l,使得d=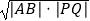 ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2016年“双十”天猫总成交金额突破1207亿元.某购物网站为优化营销策略,对11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者(其中有女性800名,男性200名)进行抽样分析.采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析,得到下表:(消费金额单位:元)
女性消费情况:
消费金额
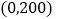
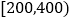
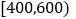
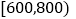
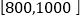
人数
5
10
15
47
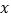
男性消费情况:
消费金额
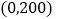
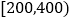
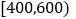
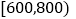
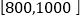
人数
2
3
10
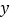
2
(1)计算
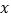 ,
,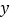 的值;在抽出的100名且消费金额在
的值;在抽出的100名且消费金额在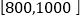 (单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写
 列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”
列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”女性
男性
总计
网购达人
非网购达人
总计
附:
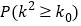
0.10
0.05
0.025
0.010
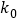
2.706
3.841
5.024
6.635
(
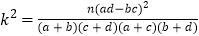 ,其中
,其中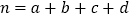 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
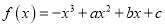 在点
在点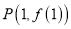 处的切线方程为
处的切线方程为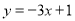 .
.(1)若函数
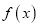 在
在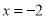 时有极值,求
时有极值,求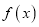 的解析式;
的解析式;(2)函数
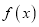 在区间
在区间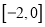 上单调递增,求实数
上单调递增,求实数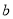 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某险种的基本保费为
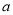 (单位:元),继续购买该险种的投保人称为续保人,
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数
0
1
2
3
4
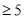
保费
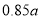
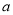
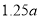
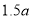
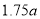

随机调查了该险种的400名续保人在一年内的出险情况,得到如下统计表:
出险次数
0
1
2
3
4
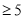
频数
120
100
60
60
40
20
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求
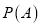 的估计值;
的估计值;(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的190%”.
求
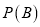 的估计值;
的估计值; (III)求续保人本年度的平均保费估计值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, 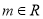 .
.(1)当
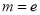 (
(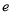 为自然对数的底数)时,求曲线
为自然对数的底数)时,求曲线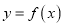 在点
在点 处的切线方程;
处的切线方程;(2)讨论函数
 的零点的个数;
的零点的个数;(3)若对任意
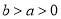 ,
, 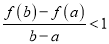 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC

(1)求证:A,B,C,P四点共圆;
(2)若∠CAD= ,AB=1,求四边形ABCP的面积.
,AB=1,求四边形ABCP的面积.
相关试题

