【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(3)为了激励同学们的学习热情,现评出一二三等奖,得分在![]() 内的为一等奖,得分在
内的为一等奖,得分在![]() 内的为二等奖, 得分在
内的为二等奖, 得分在![]() 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设![]() 为获得三等奖的人数,求
为获得三等奖的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考答案:
【答案】(1)0.06;87.5;87.5;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)根据小矩形的面积之和等于1,列出方程,求得![]() 的值,根据中位数定义估计中位数的范围,在列出方程求解中位数,再根据众数的定义,即可求解.
的值,根据中位数定义估计中位数的范围,在列出方程求解中位数,再根据众数的定义,即可求解.
(2)计算两组的人数,再计算抽取的两人在同一组的概率,即可求解;
(3)根据题意,得到随机变量服从二项分布,再利用二项分布的期望公式,即可求解.
(1)由频率分布直方图可知![]() ,解得
,解得![]() ,
,
可知样本的中位数在第4组中,不妨设为![]() ,
,
则![]() ,解得
,解得![]() ,
,
即样本的中位数为![]() ,
,
由频率分布直方图可知,样本的众数为![]() .
.
(2)由频率分布直方图可知,在![]() 与
与![]() 两个分数段的学生人数分别为
两个分数段的学生人数分别为![]() 和
和![]() ,设中两名学生的竞赛成绩之差的绝对值不大于5分为事件M,
,设中两名学生的竞赛成绩之差的绝对值不大于5分为事件M,
则事件M发生的概率为![]() ,即事件M发生的概率为
,即事件M发生的概率为![]() .
.
(3)从考生中随机抽取三名,则随机变量![]() 为获得三等奖的人数,则
为获得三等奖的人数,则![]() ,
,
由频率分布直方图知,从考升中任抽取1人,此生获得三等奖的概率为![]() ,
,
所以随机变量服从二项分布![]() ,
,
则![]() ,
,
![]() ,
,
所以随机变量的分布列为
| 0 | 1 | 2 | 3 |
| 0.343 | 0.441 | 0.189 | 0.027 |
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为 ,准线为
,准线为 ,
, 是
是 上一点,直线
上一点,直线 与抛物线交于
与抛物线交于 两点,若
两点,若 ,则
,则 ( )
( )A.
 B. 8 C. 16 D.
B. 8 C. 16 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 点测量到远处有一物体在做匀速直线运动,开始时该物体位于点
点测量到远处有一物体在做匀速直线运动,开始时该物体位于点 ,一分钟后,其位置在
,一分钟后,其位置在 点,且
点,且 ,再过二分钟后,该物体位于
,再过二分钟后,该物体位于 点,且
点,且 ,则
,则 的值等于 ( )
的值等于 ( )A.
 B.
B. C.
C. D.以上均不正确
D.以上均不正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正四面体的平面展开图,
 分别是
分别是 的中点,在这个正四面体中:①
的中点,在这个正四面体中:① 与
与 平行;②
平行;② 与
与 为异面直线;③
为异面直线;③ 与
与 成60°角;④
成60°角;④ 与
与 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,点
,点 为椭圆上一点.
为椭圆上一点. (1)求椭圆C的方程;
(2)已知两条互相垂直的直线
 ,
, 经过椭圆
经过椭圆 的右焦点
的右焦点 ,与椭圆
,与椭圆 交于
交于 四点,求四边形
四点,求四边形 面积的的取值范围.
面积的的取值范围. -
科目: 来源: 题型:
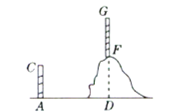
查看答案和解析>>【题目】如图,要测量山顶上的电视塔FG的高度,已知山的西面有一栋楼AC(该楼的高度低于山的高度).试设计在楼AC上测山顶电视塔高度的测量、计算方案.
相关试题

