【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 为椭圆上一点.
为椭圆上一点.
(1)求椭圆C的方程;
(2)已知两条互相垂直的直线![]() ,
,![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 四点,求四边形
四点,求四边形![]() 面积的的取值范围.
面积的的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意可得 ,解得进而得到椭圆的方程;(2)设出直线l1,l2的方程,直线和椭圆方程联立,运用韦达定理和弦长公式,分别求得|AB|,|MN|,再由四边形的面积公式,化简整理计算即可得到取值范围.
,解得进而得到椭圆的方程;(2)设出直线l1,l2的方程,直线和椭圆方程联立,运用韦达定理和弦长公式,分别求得|AB|,|MN|,再由四边形的面积公式,化简整理计算即可得到取值范围.
(1)由题意可得 ,解得a2=4,b2=3,c2=1
,解得a2=4,b2=3,c2=1
故椭圆C的方程为![]() ;
;
(2)当直线l1的方程为x=1时,此时直线l2与x轴重合,
此时|AB|=3,|MN|=4,
∴四边形AMBN面积为S![]() |AB||MN|=6.
|AB||MN|=6.
设过点F(1,0)作两条互相垂直的直线l1:x=ky+1,直线l2:x![]() y+1,
y+1,
由x=ky+1和椭圆![]() 1,可得(3k2+4)y2+6ky﹣9=0,
1,可得(3k2+4)y2+6ky﹣9=0,
判别式显然大于0,y1+y2![]() ,y1y2
,y1y2![]() ,
,
则|AB|![]()
![]()
![]() ,
,
把上式中的k换为![]() ,可得|MN|
,可得|MN|![]()
则有四边形AMBN面积为S![]() |AB||MN|
|AB||MN|![]()
![]()
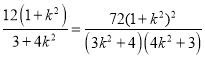 ,
,
令1+k2=t,则3+4k2=4t﹣1,3k2+4=3
则S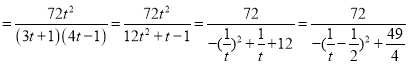 ,
,
∴t>1,
∴0![]() 1,
1,
∴y=﹣(![]() )2
)2![]() ,在(0,
,在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,1)上单调递减,
,1)上单调递减,
∴y∈(12,![]() ],
],
∴S∈[![]() ,6)
,6)
故四边形PMQN面积的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段
 ,
, ,
, ,
, ,
, ,
, ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.
(1)求图中
 的值及样本的中位数与众数;
的值及样本的中位数与众数;(2)若从竞赛成绩在
 与
与 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于 分为事件
分为事件 ,求事件
,求事件 发生的概率.
发生的概率.(3)为了激励同学们的学习热情,现评出一二三等奖,得分在
 内的为一等奖,得分在
内的为一等奖,得分在 内的为二等奖, 得分在
内的为二等奖, 得分在 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设 为获得三等奖的人数,求
为获得三等奖的人数,求 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正四面体的平面展开图,
 分别是
分别是 的中点,在这个正四面体中:①
的中点,在这个正四面体中:① 与
与 平行;②
平行;② 与
与 为异面直线;③
为异面直线;③ 与
与 成60°角;④
成60°角;④ 与
与 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
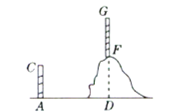
查看答案和解析>>【题目】如图,要测量山顶上的电视塔FG的高度,已知山的西面有一栋楼AC(该楼的高度低于山的高度).试设计在楼AC上测山顶电视塔高度的测量、计算方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求
 的单调区间;
的单调区间;(2)记
 的最大值为
的最大值为 ,若
,若 且
且 ,求证:
,求证: ;
;(3)若
 ,记集合
,记集合 中的最小元素为
中的最小元素为 ,设函数
,设函数 ,求证:
,求证: 是
是 的极小值点.
的极小值点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在某海滨城市A附近的海面出现台风活动.据监测,目前台风中心位于城市A的东偏南60°方向、距城市A300km的海面点P处,并以20km/h的速度向西偏北30°方向移动.如果台风影响的范围是以台风中心为圆心的圆形区域,半径为
 km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
相关试题

