【题目】在![]() 点测量到远处有一物体在做匀速直线运动,开始时该物体位于点
点测量到远处有一物体在做匀速直线运动,开始时该物体位于点![]() ,一分钟后,其位置在
,一分钟后,其位置在![]() 点,且
点,且![]() ,再过二分钟后,该物体位于
,再过二分钟后,该物体位于![]() 点,且
点,且![]() ,则
,则![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.以上均不正确
D.以上均不正确
参考答案:
【答案】C
【解析】
由题意可设PQ=x,则QR=2x,结合已知可表示∠R=30°﹣∠OPQ,在△ORQ中,△OPQ中分别利用正弦定理![]() ,OQ=
,OQ=![]() 表示OQ,变形整理,进而可得解.
表示OQ,变形整理,进而可得解.
如下图所示,物体位于点P,一分钟后,其位置在Q点,再过二分钟后,该物体位于R点

∴设PQ=x,则QR=2x,
又∵∠POQ=90°,∠QOR=60°
∠OPQ+∠R=30°,即∠R=30°﹣∠OPQ
在△ORQ中,由正弦定理得![]()
OQ=![]() 在△OPQ中,由正弦定理得OQ=
在△OPQ中,由正弦定理得OQ=![]() =xsin∠OPQ∴
=xsin∠OPQ∴![]()
整理可得,![]()
![]() ,
,![]() .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数
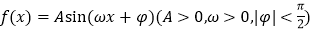 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表: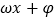

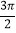
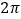
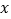

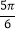

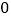
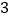
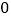
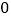
(1)请将上表数据补充完整;函数
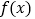 的解析式为
的解析式为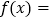 (直接写出结果即可);
(直接写出结果即可);(2)根据表格中的数据作出
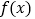 一个周期的图象;
一个周期的图象;(3)求函数
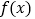 在区间
在区间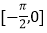 上的最大值和最小值.
上的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)指出函数
 的基本性质:定义域,奇偶性,单调性,值域(结论不需证明),并作出函数
的基本性质:定义域,奇偶性,单调性,值域(结论不需证明),并作出函数 的图象;
的图象;(2)若关于
 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若关于
 的方程
的方程 恰有
恰有 个不同的实数解,求实数
个不同的实数解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为 ,准线为
,准线为 ,
, 是
是 上一点,直线
上一点,直线 与抛物线交于
与抛物线交于 两点,若
两点,若 ,则
,则 ( )
( )A.
 B. 8 C. 16 D.
B. 8 C. 16 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段
 ,
, ,
, ,
, ,
, ,
, ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.
(1)求图中
 的值及样本的中位数与众数;
的值及样本的中位数与众数;(2)若从竞赛成绩在
 与
与 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于 分为事件
分为事件 ,求事件
,求事件 发生的概率.
发生的概率.(3)为了激励同学们的学习热情,现评出一二三等奖,得分在
 内的为一等奖,得分在
内的为一等奖,得分在 内的为二等奖, 得分在
内的为二等奖, 得分在 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设 为获得三等奖的人数,求
为获得三等奖的人数,求 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正四面体的平面展开图,
 分别是
分别是 的中点,在这个正四面体中:①
的中点,在这个正四面体中:① 与
与 平行;②
平行;② 与
与 为异面直线;③
为异面直线;③ 与
与 成60°角;④
成60°角;④ 与
与 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
相关试题

